The area under velocity-time graph gives the displacement whereas the slope of velocity-time graph at any point gives acceleration at that point. Slope is +ve if the line makes an acute angle in the anticlockwise direction with respect to the positive direction along which the independent variable increases. From the calculus, we also know that the slope of the tangent to a y vs. x graph is given by dydx If dydx is +ve then y increases with x, otherwise it decreases. Consider two persons namely Ram, and Rahim, who have gone to picnic at a nice place. Finding a beautiful place they rush towards it simultaneously. Let us take the time when they start simultaneously at t= 0 and at this instant the position of Ram and Rahim be x = 0 and x = + 48, respectively. Ram maintains a uniform velocity of +10 m/s throughout the journey whereas Rahim starts from rest and continuously accelerates with + 1m/s2
Q The position-time graph for the motions of Ram and Rahim is given by


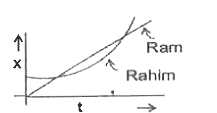
The correct Answer is:D
To solve the problem, we need to derive the position-time equations for both Ram and Rahim based on the information provided.
Step 1: Determine Ram's Position-Time Equation
Ram moves with a constant velocity of +10 m/s. The position x as a function of time t can be expressed using the formula:
x=x0+vt
Where:
- x0 is the initial position (0 m for Ram),
- v is the velocity (10 m/s for Ram),
- t is the time.
Substituting the values:
x=0+10t
Thus, Ram's position-time equation is:
xR=10t
Step 2: Determine Rahim's Position-Time Equation
Rahim starts from rest and accelerates at +1 m/s². The position x as a function of time t can be expressed using the equation of motion:
x=x0+ut+12at2
Where:
- x0 is the initial position (48 m for Rahim),
- u is the initial velocity (0 m/s for Rahim),
- a is the acceleration (1 m/s² for Rahim),
- t is the time.
Substituting the values:
x=48+0⋅t+12⋅1⋅t2
This simplifies to:
x=48+12t2
Thus, Rahim's position-time equation is:
xH=48+12t2
Step 3: Plotting the Position-Time Graphs
Now we have the equations for both Ram and Rahim:
- Ram: xR=10t
- Rahim: xH=48+12t2
1. For Ram: This is a straight line with a slope of 10, starting from the origin (0,0).
2. For Rahim: This is a parabolic curve that starts at (0, 48) and opens upwards.
Step 4: Finding the Intersection Points
To find when they meet, we set their position equations equal to each other:
10t=48+12t2
Rearranging gives:
12t2−10t+48=0
Multiplying through by 2 to eliminate the fraction:
t2−20t+96=0
Step 5: Solving the Quadratic Equation
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=1,b=−20,c=96:
t=20±√(−20)2−4⋅1⋅962⋅1
Calculating the discriminant:
t=20±√400−3842
t=20±√162
t=20±42
This gives us two possible values for t:
t=242=12andt=162=8
Conclusion
The two persons, Ram and Rahim, will meet at two different times: t=8 seconds and t=12 seconds.
---
Ram moves with a constant velocity of +10 m/s. The position x as a function of time t can be expressed using the formula:
- x0 is the initial position (0 m for Ram),
- v is the velocity (10 m/s for Ram),
- t is the time.
Rahim starts from rest and accelerates at +1 m/s². The position x as a function of time t can be expressed using the equation of motion:
- x0 is the initial position (48 m for Rahim),
- u is the initial velocity (0 m/s for Rahim),
- a is the acceleration (1 m/s² for Rahim),
- t is the time.
Now we have the equations for both Ram and Rahim:
- Ram: xR=10t
- Rahim: xH=48+12t2
2. For Rahim: This is a parabolic curve that starts at (0, 48) and opens upwards.
To find when they meet, we set their position equations equal to each other:
Using the quadratic formula t=−b±√b2−4ac2a:
t=20±√162
t=20±42
The two persons, Ram and Rahim, will meet at two different times: t=8 seconds and t=12 seconds.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II (COMPREHENSIONS-III)2videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II (MATRIX MATCH TYPE)4videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II (COMPREHENSIONS-I)3videos
KINEMATICS
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III2videos
LAWS OF MOTION
Similar Questions
The area under velocity-time graph gives the displacement whereas the slope of velocity-time graph at any point gives acceleration at that point. Slope is +ve if the line makes an acute angle in the anticlockwise direction with respect to the positive direction along which the independent variable increases. From the calculus, we also know that the slope of the tangent to a y vs. x graph is given by dydx If dydx is +ve then y increases with x, otherwise it decreases. Consider two persons namely Ram, and Rahim, who have gone to picnic at a nice place. Finding a beautiful place they rush towards it simultaneously. Let us take the time when they start simultaneously at t= 0 and at this instant the position of Ram and Rahim be x = 0 and x = + 48, respectively. Ram maintains a uniform velocity of +10 m/s throughout the journey whereas Rahim starts from rest and continuously accelerates with + 1m/s2
Q The velocity-time graph as well as the acceleration-time graph of Ram and Rahim are respectively,
 View Solution
View SolutionThe area under velocity-time graph gives the displacement whereas the slope of velocity-time graph at any point gives acceleration at that point. Slope is +ve if the line makes an acute angle in the anticlockwise direction with respect to the positive direction along which the independent variable increases. From the calculus, we also know that the slope of the tangent to a y vs. x graph is given by dydx If dydx is +ve then y increases with x, otherwise it decreases. Consider two persons namely Ram, and Rahim, who have gone to picnic at a nice place. Finding a beautiful place they rush towards it simultaneously. Let us take the time when they start simultaneously at t= 0 and at this instant the position of Ram and Rahim be x = 0 and x = + 48, respectively. Ram maintains a uniform velocity of +10 m/s throughout the journey whereas Rahim starts from rest and continuously accelerates with + 1m/s2
Q Shown is a graph of either position or velocity-time graph
Choose the correct alternative.View Solution
Knowledge Check
- Question 1 - Select One
The area under a velocity-time graph gives :
ADisplacementBChange in velocityCAccelerationDSpeed - Question 2 - Select One
Area under a velocity-time graph gives
Athe time taken by a moving objectBthe distance travelled by a moving objectCthe acceleration of moving objectDthe retardation of a moving object - Question 3 - Select One
The area under acceleration-time graph gives
ADistance travelledBChange in accelerationCForce actingDChange in velocity
What does the slope of velocity-time graph represent ?
View SolutionDraw the velocity-time graph for uniformly accelerated motion. Show that slope of the velocity-time graph gives acceleration of the object.
View SolutionThe slope of velocity-time graph for uniform motion of an object is
View SolutionThe area under the acceleration-time (a-t) graph gives
View SolutionAssertion: Area under velocity-time graph give displacement.
Reason: Area under acceleration-time graph give velocity.View Solution

