Three particles each of mass 'm' can slide on fixed frictionless circular track in the same horizontal plane as shown in the figure. Particle m1 moves with velocity v0 and hits particle m2, the coefficient of restitution being θ=1/2. AsSigmae m2 and m3 are initially in rest and lie along a radial line before impact and the spring is initially Unstretched. Then,
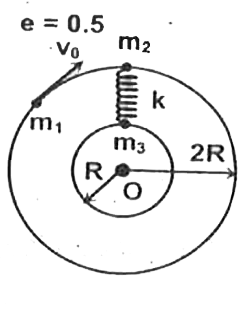
The velocity of m3 when extension in the spring is maximum
110v0
310v0
710v0
none of these
The correct Answer is:B
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - NUMERICAL BASED QUESTIONS
4 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - MATRIX MATCH TYPE
6 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE
1 Video
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
Three particles each of mass m can slide on fixed frictionless horizontal circular tracks in the same horizontal plane as shown in the figure. The coefficient of restitution being e=0.5. Assuming that m2 and m3 are at rest initially and lie along a radial line before impact and the string is initially unstretched, then maximum extension in spring in subsequent motion

View SolutionA particle moving with velocity (2ˆi−3ˆj) m/s collides with a surface at rest in xz–plane as shown in figure and moves with velocity (2ˆi+2ˆj) m/s after collision. Then coefficient of restitution is :
View Solution
Knowledge Check
There particles each of mass m can slide on fixed frictioless circular tracks in the same horizontal plane as shown. Particle m1(=m) moves with velocity v0 and hits particle m2(=m), the cofficient of restitution being e=0.5 . Assume that m2 and m3(=m) are at rest initially and lie along a radial line before impact, and the spring is initially unstretched.

Velocity of m2 immediately after impact isAv04B3v04Cv02D3v02Three particles each of mass m can slide on fixed frictionless horizontal circular tracks in the same horizontal plane as shown in the figure. The coefficient of restitution being e=0.5. Assuming that m2 and m3 are at rest initially and lie along a radial line before impact and the string is initially unstretched, then maximum extension in spring in subsequent motion
 A34V0√mkB34V0√m5kC34V0√2m5kD35V0√mk
A34V0√mkB34V0√m5kC34V0√2m5kD35V0√mkA particle moving with velocity (2ˆi−3ˆj) m/s collides with a surface at rest in xz–plane as shown in figure and moves with velocity (2ˆi+2ˆj) m/s after collision. Then coefficient of restitution is :
 A23B1C√813D45
A23B1C√813D45
A particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass'm' is projected with velocity v0 at an angle 'α' with the horizontal. The coefficient of restitution for any of its impact with the smooth ground is e.

Find total time taken by the particle before it stops moving vertically?
View SolutionA particle of mass'm' is projected with velocity v0 at an angle 'α' with the horizontal. The coefficient of restitution for any of its impact with the smooth ground is e.

Find total time taken by the particle before it stops moving vertically?
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
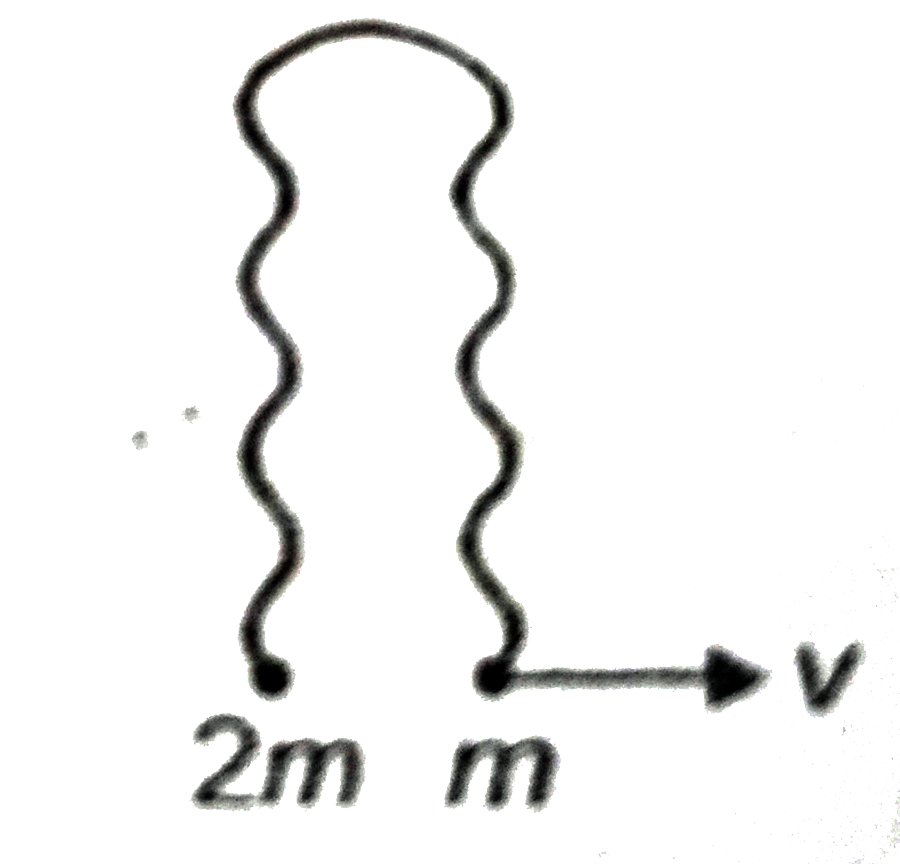
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.

View Solution
