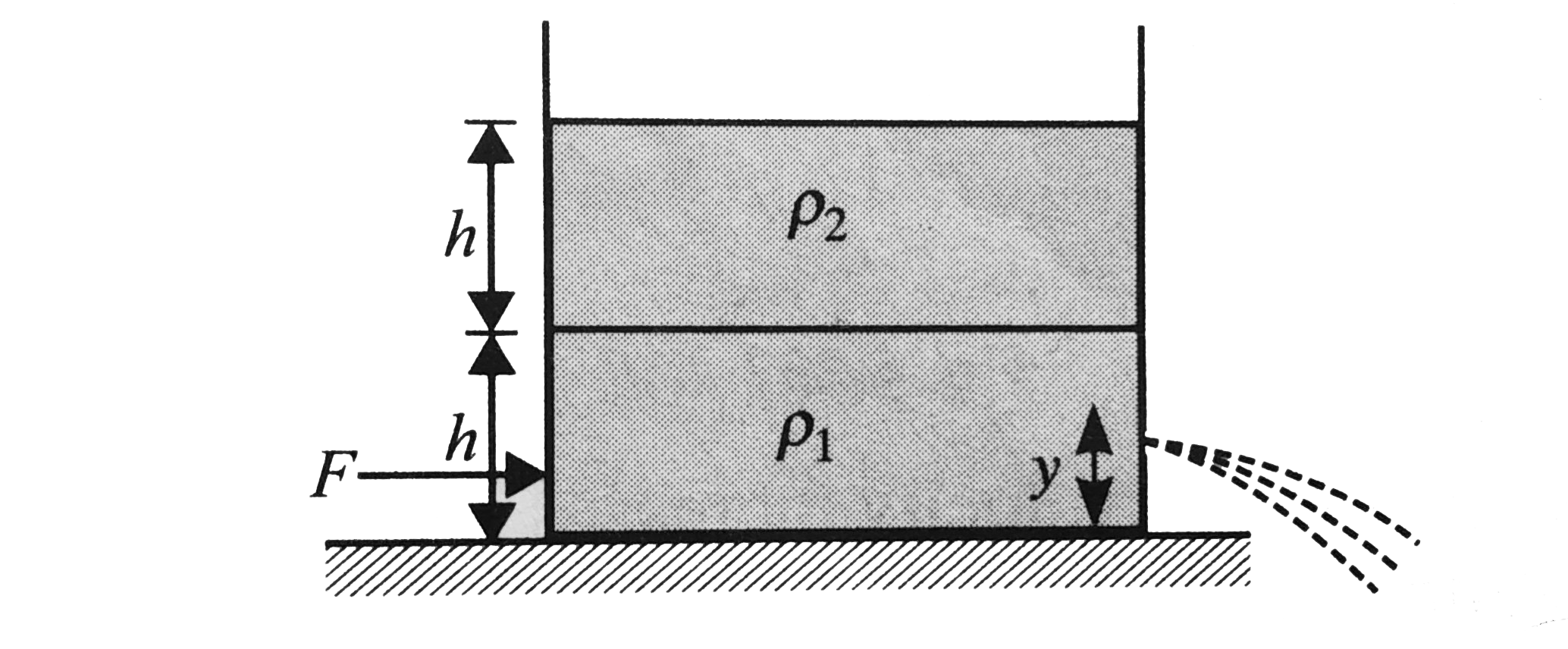
A cylindrical tank having cross - sectional area A=0.5m2 is filled with two liquids of density ρ1=900 kg m−3andρ2=600 kg m−3 , to a height a =6cm2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g=10ms−2)
Minimum and maximum values of F to keep the cylinder in static just after the water starts to spill through the hole . If the co - efficient of static friction between contact surfaces is 0.01
0,40 N
5.4N , 52.2 N
0 , 70 N
0, 52.2 N
Total mass of the liquid in the cylinder is
m=Ahρ1+Ahρ2=450Kg
Limiting friction =μmg=45N
∴F< limiting friction , therefore , minimum force required is zero .
Consider free body diagram for mximum vertical froces .
N = mg
Now considering horizontal forces ,
N = mg
Fmax=F+μN
or Fmax=52.2N
Topper's Solved these Questions
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - LINKED COMPREHENSION TYPE II
2 Videos
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - LINKED COMPREHENSION TYPE III
2 Videos
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - LINKED COMPREHENSION TYPE
2 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
Similar Questions
The force of interaction between the molecules of same substance is called cohesive force hile force of interaction between molecules of different substances is called adhesive force . Both the forces are attracive and have a range of about 10 A . If we consider a molecule . A well inside a liquid we find that it is equally attracted by the surrounding molecules in all the directions ( with a sphere of radius 10 Å ) and so it does not experience any resultant force . On or near the surface of a liquid , the molecules do not exist on the free side and so a molecule ( say B ) experiences a resultant force vertically downwards into the liquid . For this reason , the molecules of the surface have a tendency to go into the liquid . Thus , the surface tends to contract and gives rise to surface tension .
As surface molecules like B experience a net downward force of cohension and have tendency to go down , so in increasing the area of the surface more molecules are to be shifted to the surface from inside . Thus , more mechnical work will have to be done against the net downward force of cohension . This work is stored by the molecules in the surfaces as potential energy called free surface energy .
Furthermore , molcules like P , in contact with the liquid will stick to the solid surface , i.e will meet it if the force of adhesion A is greater than net force of cohension C . The liquid will not the solid surface if C>A
Also , molecules like Q at the surface in contact with the solid will experience a net force of cohension CR . If adhesion A is greater then cohension CR , the resultant force will be F . As the liquid can't support tangential force , F must be perpendicular to the surface of the liquid . So , the menisus will be concave and the angle of contact will be acute (>90∘) . However , if adhesion is lesser than cohension , the resultant force F will be directed into the liquid and so the menisus ( which is perpendicular to F as liquid support tangential force ) will be convex and the angle of contact will be obtuse (>90∘)
A liquid particle B , which is present in the vicinity particle A can exert a force on A if the distance of B from A is
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is

View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg = 10 ms^(-2)).
The horizontal force required to keep the cylinder in static equilibrium, on a smooth horizontal plane is
View SolutionAn infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.

View SolutionTwo resistors along with errors are kown as
R1=(30±3)Ω
R2=(60±3)Ω
column - I lists four alagebratic functions of R1R2 column -II lists corresponding errors where as column -III lisits the absolute errors

pick the correct option
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg = 10 ms^(-2)).
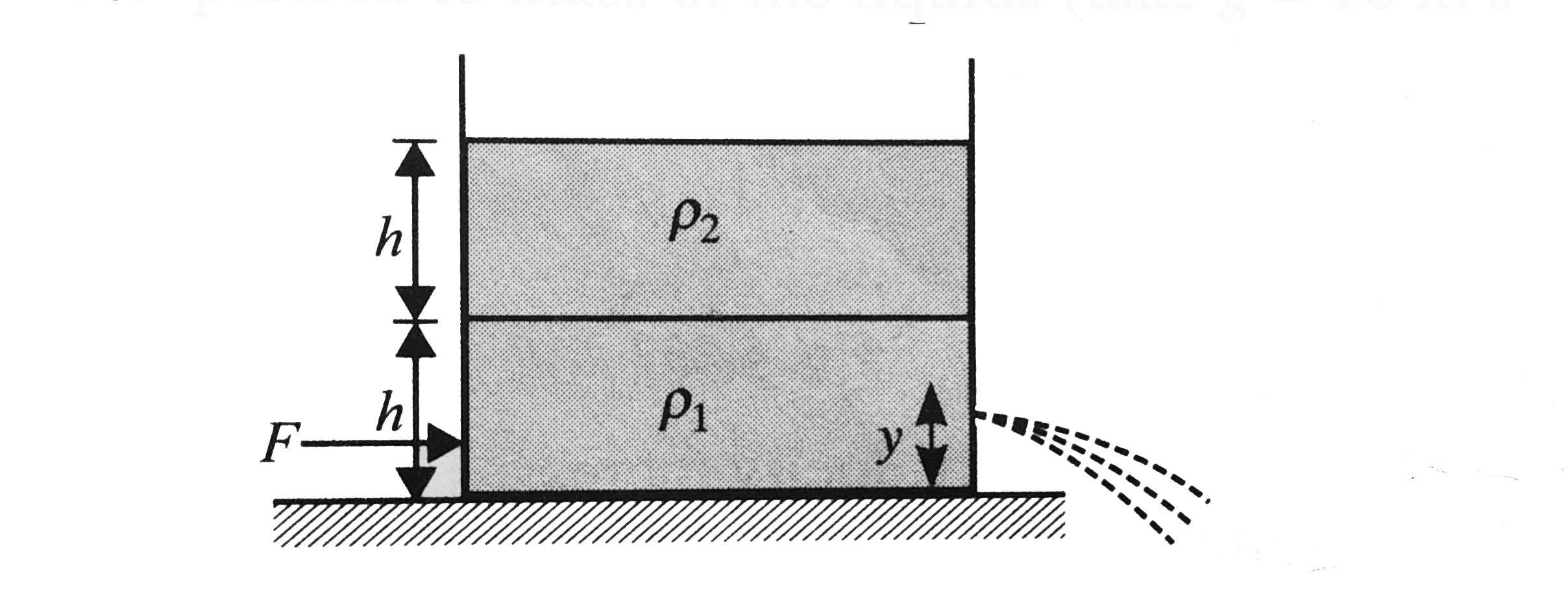
The velocity of efflux is
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg = 10 ms^(-2)).

The velocity of efflux is
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg=10ms−2).
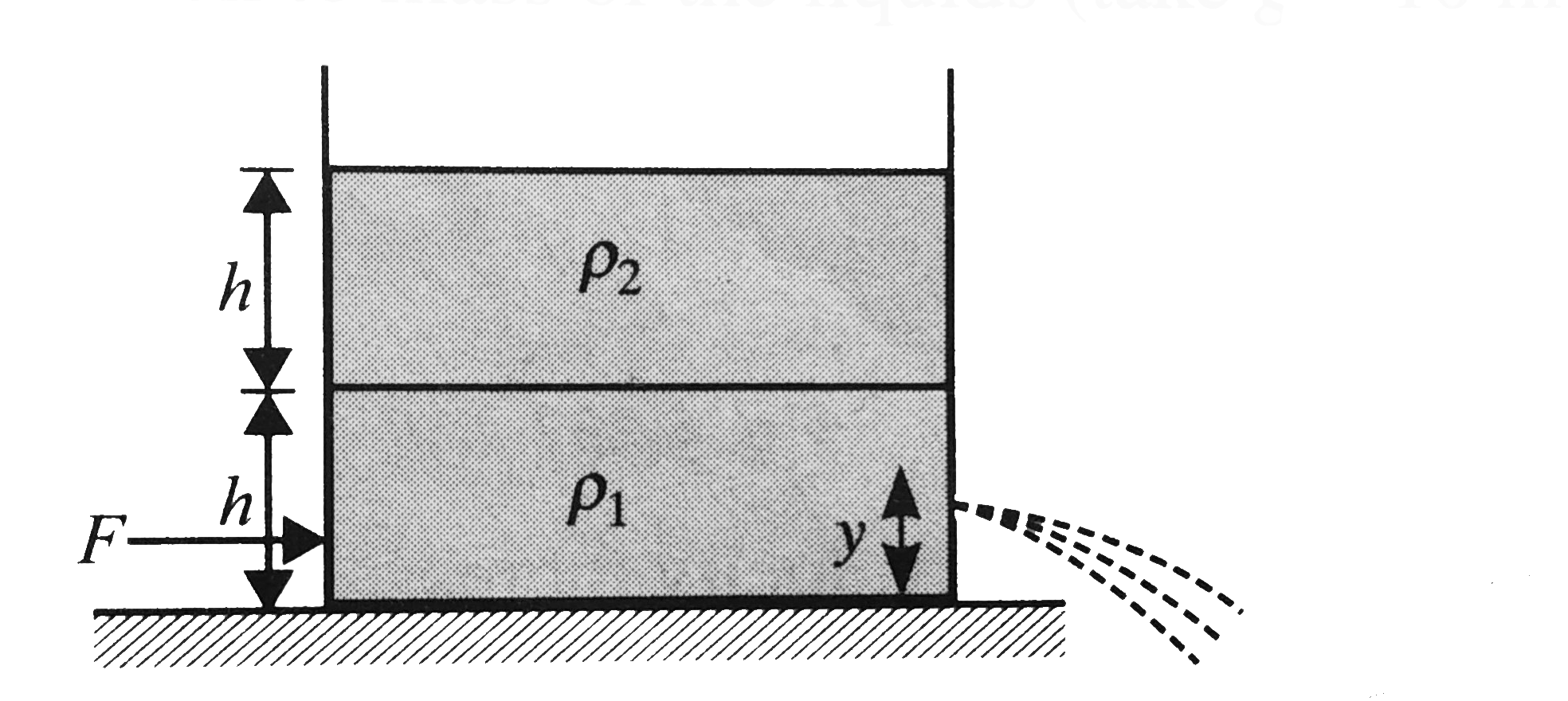
The velocity of efflux is
View SolutionA cylinderical tank having cross sectional area ^^=0.5m^(2) is filled liquids of densities rho_(1)=900kgm^(3)&rho_(2)=600kgm^(3) to a height h=60cm as shown in the figure a small hole having area a=5cm^(2) is made in right vertical wall at a height y=20cm from the bottom calculate. (i). velocity of efflux (ii). horizontal force F to keep the cylinder in static equilibrium if it is placed on a smooth horizontal plane (iii). minimum and maximum value of F to keep the cylinder at rest. The coefficient of friction between cylinder and the plane is mu=0.1 (iv). velocity of the top most layer of the liquid column and also the velocity of the boundary separating the two liquids.
View SolutionTwo immisible liquids are pured in a U-tube having densities rho_(1) = 1.0 xx 10^(2) kg//m^(2) and rho_(2)2.0 xx 10^(3) kg//m^(3) . Find the ratio of heights (of the liquids above their interface) (n_(1))/(h_(2))
View SolutionA rectangular tank of base area 100 m2 has a height of 2 m. Calculate the thrust at the bottom of the tank, if it is filled upto the brim with water of density 103 kg m−3.
View SolutionA cylindrical tank having cross - sectional area A = 0.5 m^(2) is filled with two liquids of density rho_(1)= 900 " kg "m^(-3) and rho_(2) = 600 " kg "m^(-3) , to a height h = 60 cm^(2) each.A small hole having area a=5 cm^2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g = 10 ms^(-2) ) Horizontal force F to keep the cylinder in static equilibrium , if it is placed on a smooth horizontal thrust exerted by fluid jet . But that is equal to mass flowing per second xx change in velocity of this mass :. " " F = (avrho) (v-0) = a rho v^(2) or F = 7.2 N
View SolutionCalculate the pressure exerted by a column of water of height 0.85 m (density of water, rho_(w) = 1000 kg m^(-3) ) and kerosene of same height (density of kerosene, rho_(k) = 800 kg m^(-3))
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (Take g = 10 ms^(-2)).

The velocity of efflux is
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg=10ms−2).

(i) horizontal force F to keep the cylinder in static equilibrium, if it is placed on a smooth horizontal plane and (ii) minimum and maximum values of F to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is µ = 0.01. (g = 10 ms –2 )
View SolutionA rectangular tank of base area 100 m^(2) has a height of 2 m. Calculate the thrust at the bottom of the tank, if it is filled upto the brim with water of density 10^(3) kg m^(-3) .
View Solution
