When a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical vloume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48stal

This is called Poisecuille's equation .
The volume of the liquid flowing per sec across the cross - section of the tube is .
πR2v0
(πR2v0)/2
(πR2v0)/3
(πR2v0)/4
The correct Answer is:B
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT COMPREHENSION COMPREHENSION -III2videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT COMPREHENSION COMPREHENSION -IV2videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT PROBLEMS COMPREHENSION -I3videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example14videos
ELECTROSTATICS
- BOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE3videos
GENERAL PHYSICS
Similar Questions
A wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If level of liquid starts decreasing slowly, when the level of liquid is at a height h1 above the cylinder, the block just start moving up. Then the value of h1 is01:16View SolutionThe curved wall of a dam is described by the equation
x2=2y
The coordinates of point A are (4m,8m) . The width of the dam is 2m and the fluid is water of density 1×103kg/m3
Atmospheric pressure is 1.0×105 Pa
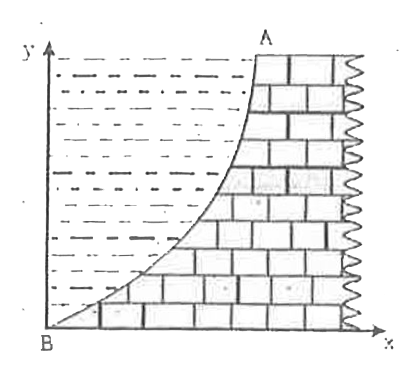
The horizontal component of the force applied by the liquid on the surface AB is (g=10ms−2)01:42View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mrcury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
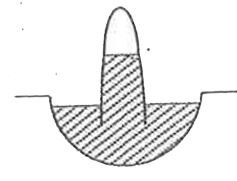
If a small hole is made at point P in the barometer tube , then
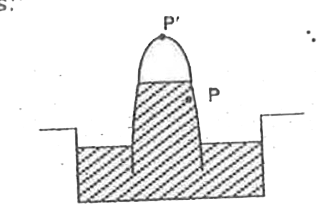 02:44View Solution
02:44View SolutionAn infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.
 03:56View Solution
03:56View SolutionTwo resistors along with errors are kown as
R1=(30±3)Ω
R2=(60±3)Ω
column - I lists four alagebratic functions of R1R2 column -II lists corresponding errors where as column -III lisits the absolute errors

pick the correct option04:37View SolutionThe viscous force acting between two layers of a liquid is given by F/A=eta(dv)/(dz) . This F/A may be caled
02:45View SolutionAccording to Newton, the viscous force acting between liquid layers of area A and velocity gradient (Deltav)/(Deltaz) is given by F =- eta A (dv)/(dz) , where eta is constant called
03:33View SolutionThe viscous force acting on adjacent layers of liquid is
01:26View SolutionThe viscous force acting between 2 layers of a liquid is given by FA=ηdvdz = This F/A may be called
View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by F = - eta A (dv)/(dx) where A is the area of the layer (dv)/(dx) is the velocity gradient at the layer and eta is the coefficient of viscosity of the liquid. If f is the frictional force between a solid sliding over another solid, and F is the viscous force when a liquid layer slides over another, then :
02:12View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by F = - eta A (dv)/(dx) where A is the area of the layer (dv)/(dx) is the velocity gradient at the layer and eta is the coefficient of viscosity of the liquid. The dimensional formula for the coefficient of viscosity is :
02:12View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
A river is 5 m deep. The velocity of water on its surface is 2ms−1 If the coefficient of viscosity of water is 10−3Nsm−2 , the viscous force per unit area is :01:25View SolutionAccording to Newton, the viscous force acting between liquid layers of area A and velocity gradient Δv/Δz is given by F=−ηAΔvΔz where η is constant called coefficient of viscosity. The dimension of η is :
02:12View SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by F = - eta A (dv)/(dz) where , ete = coefficient of viscosity , A = surface area of adjacent layers in contact , (dv)/(dz) = velocity gradient Now , a viscous liquid having coefficient of viscosity eta is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero . - eta 2pirl (dv)/(dr) = Ppir^(2) - int _(v)^(0),dv = P/(2 eta l) int_(tau)^(R) rdr ( :' layer in contact with the tube is stationary ) v = v_(0) (1- (r^(2))/(R^(2))) , where v_(0) = (PR^(2))/(4nl) :. " " Q = (piPR^(4))/(8sta l) This is called Poisecuille's equation . The viscous force on the cylindrical volume of the liquid varies as
04:19View SolutionAccording to Newton, the viscous force acting between liquid layers of area A and velocity gradient ΔvΔz is given by F=−ηAdvdz, where η is constant called coefficient of viscosity . The dimensional formula of its
02:12View SolutionAccording to Newton, the viscous force acting between liquid layers of area A and velocity gradient ΔvΔz is given by F=−ηAdvdz, where η is constant called coefficient of viscosity . The dimensional formula of its
01:34View Solution

