A fluid of density ρ and viscosity η is kept in a container .The container is accelerating in horizontal direction with acceleration a . A Small solid sphere of radius r and density ρ/2 is held at the base of the container and released The distance travelled by the sphere in attaining half the terminal velocity is s=ρr2vτkη[In(2)−12] . Find the value of k .
![A fluid of density rho and viscosity eta is kept in a container .The container is accelerating in horizontal direction with acceleration a . A Small solid sphere of radius r and density rho//2 is held at the base of the container and released The distance travelled by the sphere in attaining half the terminal velocity is s = (rho r^(2) v(tau))/(k eta) [ In (2) - 1/2 ] . Find the value of k .](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIITJEE_PHY_MB_02_C02_E06_001_Q01.png)
The correct Answer is:9
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The gravitational acceleration on the surface of earth of radius R and mean density ρ is
A(4π/3)GR2ρB(4π2/3)GR2ρC(2π2/3)GR2ρD(4π/3)GRρ - Question 2 - Select One
What is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
A105176R2ρB105176R2ρC176105R2ρD186105R2ρ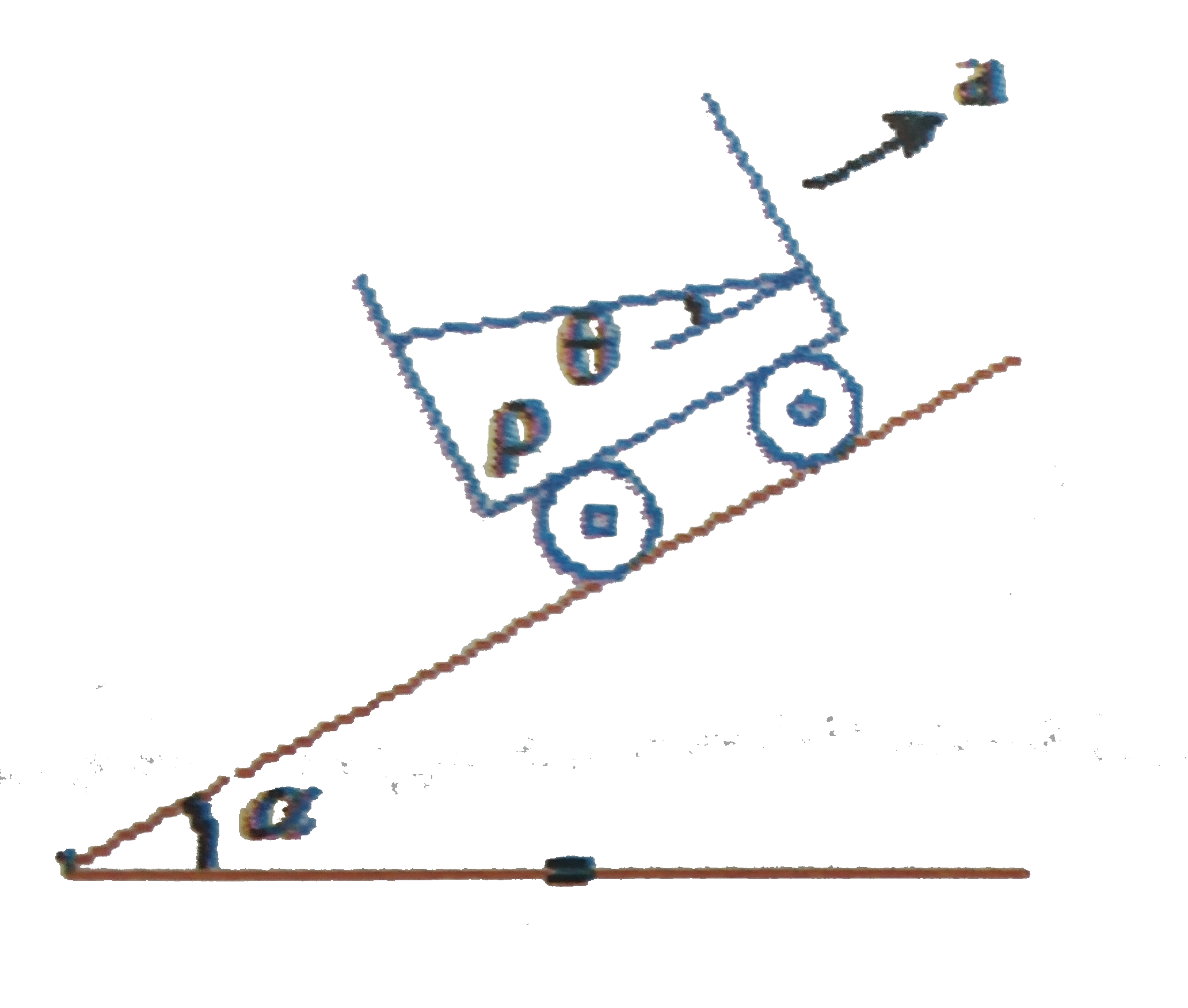 - Question 3 - Select One
A fluid container is containing a liquid of density ρ is accelerating upward with acceleration a along the inclined plane of inclination α as shown in the figure. Then the angle of inclination θ of free surface isAtan−1[agcosα]Btan−1[a+gsinαgcosα]Ctan−1[a−gsinαg(1+cosα)]Dtan−1[a−gsinαg(1−cosα)]
A Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionA Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
View Solution