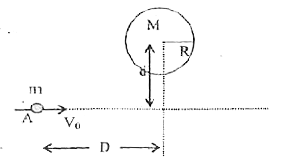
With what speed $v_{0}$ should a body be projected as shown in the figure, with respect to a planet of mass $M$ so that it would just be able to graze the planet and escape ? The radius of the planet is $R$ . (Assume that the planet is fixed ).

Video Solution

Text Solution

Verified by Experts

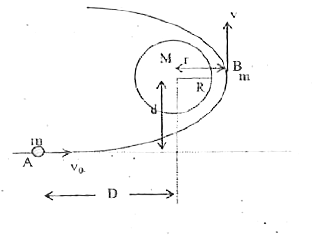
By conservation of angular momentum we obtain
$m v_{0} d = m v r$
$\Rightarrow v = \frac{m v_{0} d}{m r} = v_{0} (d / r)$
By conservation of energy at $A$ and $B$ , we have
$\frac{1}{2} m v_{0}^{2} - \frac{G M m}{\sqrt{D^{2} + d^{2}}} = \frac{1}{2} m v^{2} - \frac{G M m}{r}$
When $r \approx R$ we obtain,
$\frac{1}{2} m v_{0}^{2} - \frac{G M m}{\sqrt{D^{2} + d^{2}}} - \frac{1}{2} m . \frac{v_{0}^{2} d^{2}}{R^{2}} - \frac{G M m}{R}$
$\frac{1}{2} m v_{0}^{2} (\frac{d^{2}}{R^{2}} - 1) = G M m [\frac{1}{R} - \frac{1}{\sqrt{D^{2} + d^{2}}}]$
$\Rightarrow v_{0} = \sqrt{\frac{2 G M (\frac{1}{R} - \frac{1}{\sqrt{D^{2} + d^{2}}})}{(\frac{d^{2}}{R^{2}} - 1)}}$

Updated on:21/07/2023