A system consists of a thin ring of radius R and a very long uniform wire oriented along axis of the ring with one of its ends coinciding with the centre of the ring. If mass of ring be M and mass of wire be λ per unit length, calculate interaction force between the ring and the wire.
The force of interaction due to ring on the element dx is
dF=GM(dm)(r2+x2)cosα where, cosα=x√x2+r2
⇒dF=Gmxλdx(r2+x2)3/2
⇒F=Gmλ∫∞0xdx(r2+x2)3/2=GMλ∫π/20r2tanθsec2θdθr3sec3θ
=GMλr∫π/20sinθdθ=GMλr|−cosθ|π/20=GMλr

Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assigment problems (Subjective) (level I)14videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assigment problems (Subjective) (level II & III)15videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Matrix match type2videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based61videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
Similar Questions
A system consits fo a thin charged wire ring of radius R and a very long uniformly charged thread oriented along the axis of the ring, with one of its ends coinciding with the centre of the ring. The total charge of the ring, with one of the ring so equal to q. The charge of the thread (per unit length) is equal to λ. Find the interaction froce between the ring and the thread.
View SolutionA ring of radius R carries a charge q uniformly distribited over it. A long thin wire carrying charge λper unit length of it is held along its axis with one end coinciding with the centre of the ring. Find the interaction force between the ring and the thread.
View Solution
Knowledge Check
- Question 1 - Select One
Consider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
AGmr2B2Gm√3r2C2Gm3√3r2DGm2r2 - Question 2 - Select One
The M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
A12MR2B32MR2CMR2D2MR2 - Question 3 - Select One
A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
AMl4π2BMl2πCMl4πDMl24π2
A quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
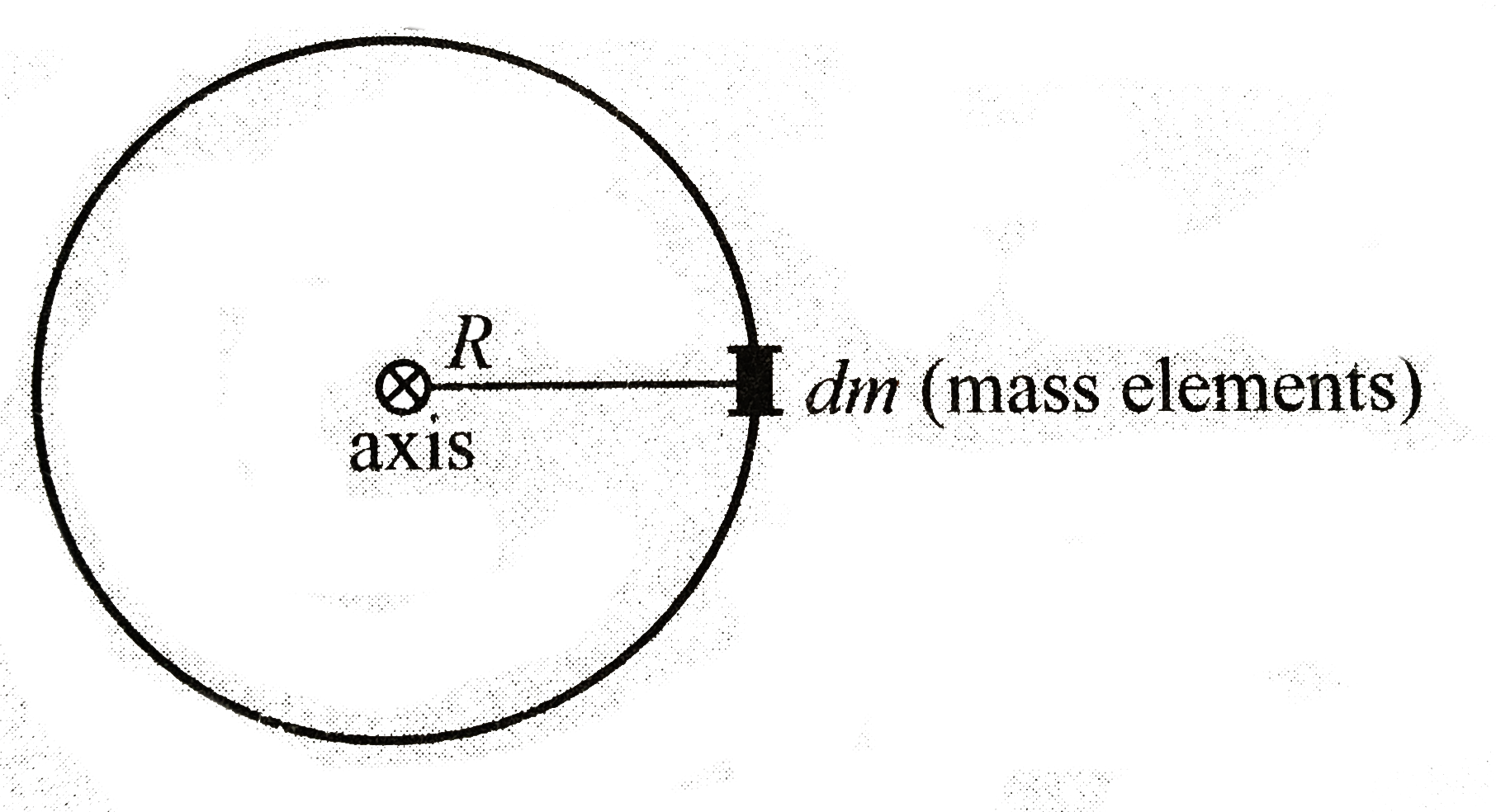 View Solution
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA very long uniformly charged wire oriented along the axis of a circular ring of radius R rests on its centre with one of the ends (as shown in figure). The linear charge density on the wire is λ. Evalute the flux of the vector →E across the circle area.
 View Solution
View SolutionCalculate the moment of inertia of
a. a ring of mass M and radius R about an axis coinciding with the diameter of the ring.
b. as thin disc about an axis coinciding with the diameter.View Solution

