Let V and E be the gravitational potential field. Then select the correct alternative (s)
the plot of E against r (distance from centre) is discontinuous for a spherical shell
the plot of V against r is continous for a spherical shell
the plot of E against r is discontinuous for a solid sphere
the plot of V against r is continuous for a solid sphere
The correct Answer is:A, B, D
To solve the problem regarding the gravitational potential field V and the gravitational field E, we need to analyze the behavior of these fields for both a spherical shell and a solid sphere.
1. Understanding Gravitational Field E and Potential V:
- The gravitational field E is defined as the force per unit mass experienced by a small test mass placed in the field.
- The gravitational potential V at a point is defined as the work done in bringing a unit mass from infinity to that point without any acceleration.
2. Behavior of E and V for a Spherical Shell:
- Inside the Spherical Shell:
- The gravitational field E inside a spherical shell is zero.
- The gravitational potential V is constant and equal to the potential on the surface of the shell.
- Outside the Spherical Shell:
- The gravitational field E behaves as if all the mass were concentrated at the center, following E=GMr2.
- The gravitational potential V decreases with distance and follows V=−GMr.
3. Behavior of E and V for a Solid Sphere:
- Inside the Solid Sphere:
- The gravitational field E increases linearly with distance from the center, given by E=GMR3r where r is the distance from the center.
- The gravitational potential V is given by V=−GM2R+GMR3r2, which is continuous and has a maximum at the center.
- Outside the Solid Sphere:
- Similar to the shell, the gravitational field E behaves as E=GMr2.
- The gravitational potential V behaves as V=−GMr.
4. Analyzing the Plots:
- For the spherical shell:
- E is discontinuous at the surface (it jumps from 0 to a non-zero value).
- V is continuous across the surface.
- For the solid sphere:
- E is continuous throughout.
- V is also continuous throughout.
5. Selecting the Correct Alternatives:
- The correct statements based on the analysis are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of E against R for a solid sphere is continuous.
- The plot of V against R is continuous for a solid sphere.
Conclusion:
The correct alternatives are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of V against R is continuous for a solid sphere.
- The gravitational field E is defined as the force per unit mass experienced by a small test mass placed in the field.
- The gravitational potential V at a point is defined as the work done in bringing a unit mass from infinity to that point without any acceleration.
- Inside the Spherical Shell:
- The gravitational field E inside a spherical shell is zero.
- The gravitational potential V is constant and equal to the potential on the surface of the shell.
- Outside the Spherical Shell:
- The gravitational field E behaves as if all the mass were concentrated at the center, following E=GMr2.
- The gravitational potential V decreases with distance and follows V=−GMr.
- Inside the Solid Sphere:
- The gravitational field E increases linearly with distance from the center, given by E=GMR3r where r is the distance from the center.
- The gravitational potential V is given by V=−GM2R+GMR3r2, which is continuous and has a maximum at the center.
- Outside the Solid Sphere:
- Similar to the shell, the gravitational field E behaves as E=GMr2.
- The gravitational potential V behaves as V=−GMr.
- For the spherical shell:
- E is discontinuous at the surface (it jumps from 0 to a non-zero value).
- V is continuous across the surface.
- For the solid sphere:
- E is continuous throughout.
- V is also continuous throughout.
- The correct statements based on the analysis are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of E against R for a solid sphere is continuous.
- The plot of V against R is continuous for a solid sphere.
The correct alternatives are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of V against R is continuous for a solid sphere.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question2videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assigment problems (Objective) (level-I) Assertion & Reasoning type2videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based61videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
Similar Questions
Let V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)NoneView SolutionLet VG and EG denote gravitational potential and field respectively, then choose the wrong statement.
View Solution
Knowledge Check
- Question 1 - Select One
Select the correct alternatives :
AWork done by kinetic friction on a body always results in a loss of its kinetic energy.BWork done on a body, in the motion of that body over a close loop is zero for every force in nature.CTotal mechanical energy of a system is always conserved no matter what type of internal and ecternal forces on the body are present.DWhen total work done by a conservative force on the system is positive then the potential energy associated with this force decreases. - Question 2 - Select One
Select the incorrect alternatives(s):
Ahas a fixed valueBmay be zeroCmay be infiniteDmay be negative - Question 3 - Select One or More
For the given circuit, select the correct alternative(s)
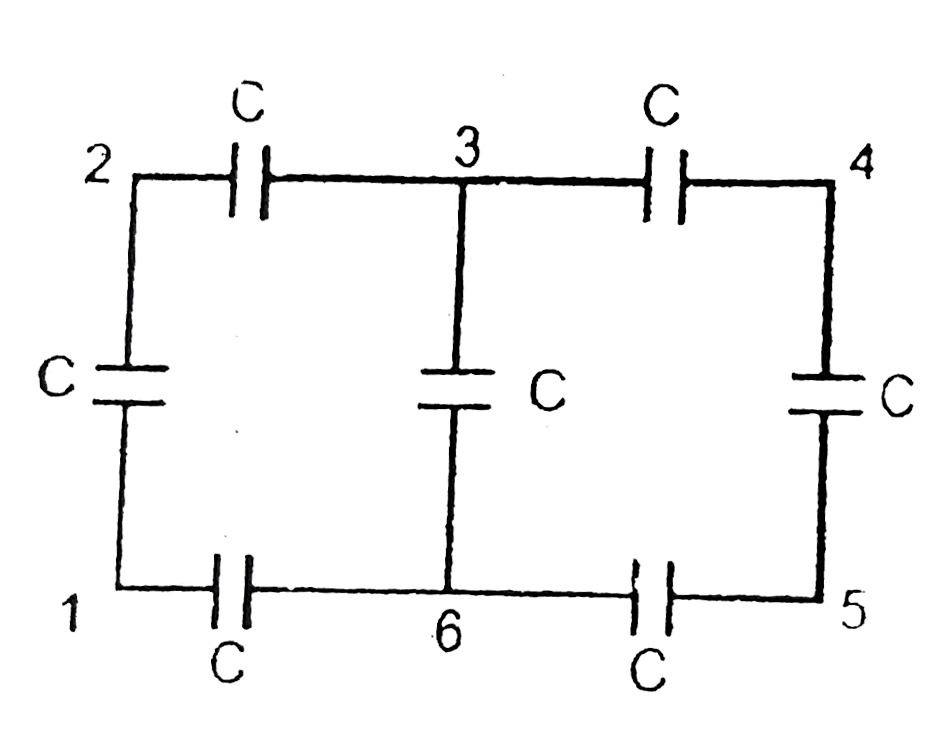 AThe equivalent capacitance between points 1&2is15C11BThe equivalent capacitance between poits 3&6is5C3CThe equivalent capacitance between points 1&3is15C14DThe equivalent capacitance between points 3&5is14C15
AThe equivalent capacitance between points 1&2is15C11BThe equivalent capacitance between poits 3&6is5C3CThe equivalent capacitance between points 1&3is15C14DThe equivalent capacitance between points 3&5is14C15
The S.I. unit of gravitational potential is
View SolutionLet VG and EG denote gravitational potential and field respectively, then choose the wrong statement.
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.View SolutionLet V and E denote the gravitational potential and gravitational field at a point. It is possile to have
View Solution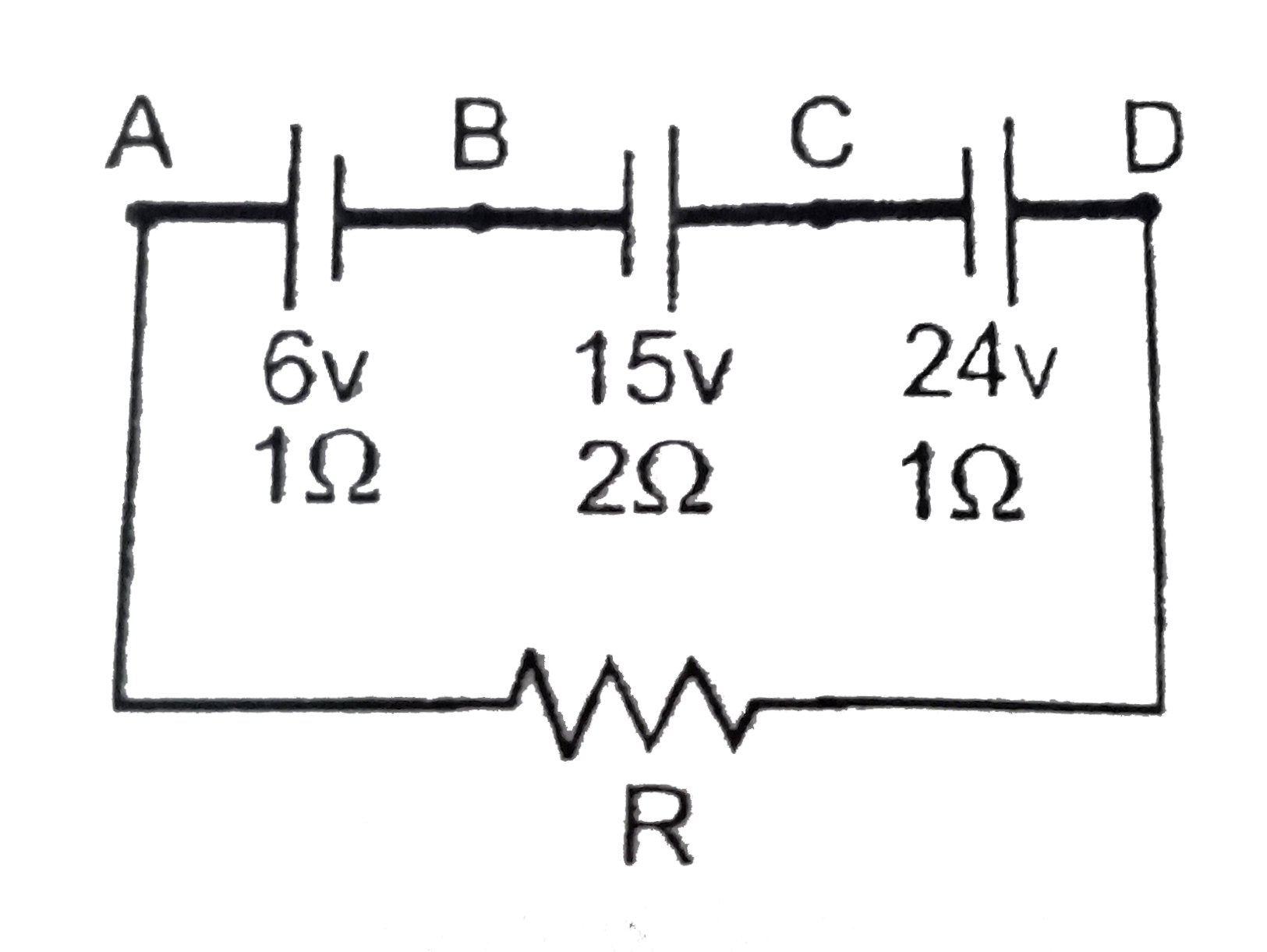
In the given circuit potential of the point A is 9 V higher than potential of the point B. Choose correct alternative (s)View Solution

