A rod of mass m and length l is free to rotate in a vertical plane about fixed horizontal axis O passing through one end as shown in the figure. A sphere of mass $\frac{m}{4}$ hits the rod elastically with horizontal speed $v_{0}$ at a distance $\frac{2 l}{3}$ from O. Before collision, the rod is at rest in vertical position. If we consider the sphere and the rod as a system, then gravity and force due to axis O are external forces. For the rod alone, force exerted by O, gravity and impact force are all external forces. Similar conclusion can be drawn for the sphere. Net external force on any system is equal to the product of the mass of the system and the acceleration of the centre of the mass of the system.

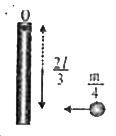
The maximum angular deflection of the rod from the vertical after the collision is

$θ = {cos}^{- 1} (1 - \frac{5}{16} \frac{v_{0}^{2}}{g l})$

$θ = {sin}^{- 1} (1 - \frac{3}{16} \frac{v_{0}^{2}}{g l})$

$θ = {cos}^{- 1} (1 - \frac{3}{16} \frac{v_{0}^{2}}{g l})$

$θ = {sin}^{- 1} (1 - \frac{5}{16} \frac{v_{0}^{2}}{g l})$

Text Solution

Verified by Experts

The correct Answer is:C

$\frac{m}{4} . \frac{2 l}{3} . v_{0} = \frac{m l^{2}}{3} ω + \frac{m}{4} v_{1} \frac{2 l}{3}$
$2 v_{0} = \frac{8 ω l}{3} \Rightarrow ω = \frac{3 v_{0}}{4 l}$
$v_{1} = \frac{2 ω l}{3} - v_{0}$
$v_{1} = \frac{- v_{0}}{2}$
$\frac{m g l}{2} (1 - cos θ) = \frac{1}{2} I ω^{2}$

Updated on:21/07/2023

Class 12 PHYSICS ROTATIONAL MECHANICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
Question 2 - Select One
An uniform rod of mass $m = 30 k g$ and length $l = 0.80 m$ is free to rotate about a horizontal axis $O$ passing through its centre. A particle $P$ of mass $M = 11.2 k g$ falls vertically through a height $h = \frac{36}{245} m$ and collides elastically with the rod at a distance $\frac{l}{4}$ from $O$ . at the instant of collision the rod was stationary and was at angle $α = 37^{\circ}$ with horizontal as shown in figure

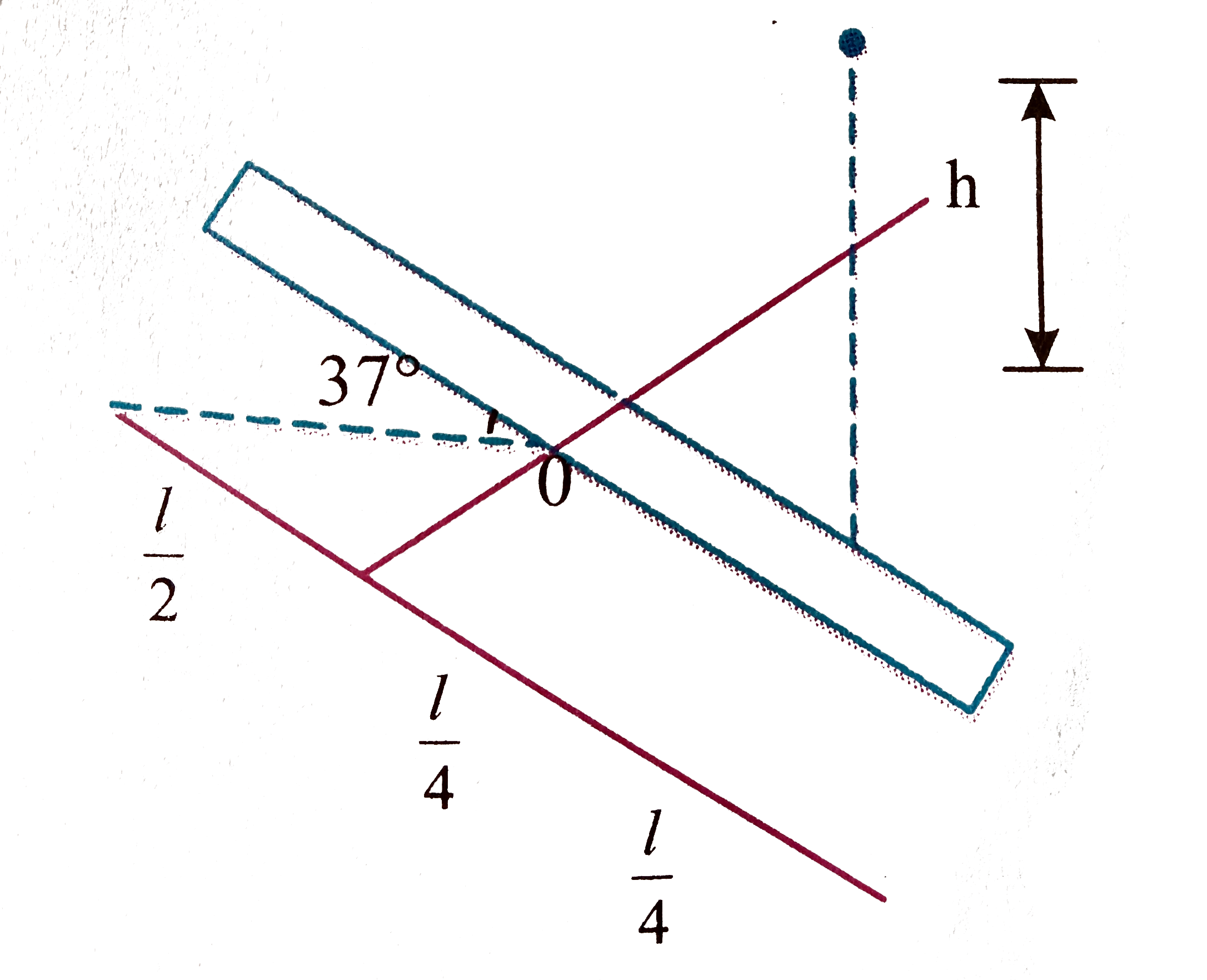
Calculate velocity of the rod just after collision is
A $1 r a d / s$
B $3 r a d / s$
C $2 r a d / s$
D $4 r a d / s$
Question 3 - Select One
An uniform rod of mass $m = 30 k g$ and length $l = 0.80 m$ is free to rotate about a horizontal axis $O$ passing through its centre. A particle $P$ of mass $M = 11.2 k g$ falls vertically through a height $h = \frac{36}{245} m$ and collides elastically with the rod at a distance $\frac{l}{4}$ from $O$ . at the instant of collision the rod was stationary and was at angle $α = 37^{\circ}$ with horizontal as shown in figure

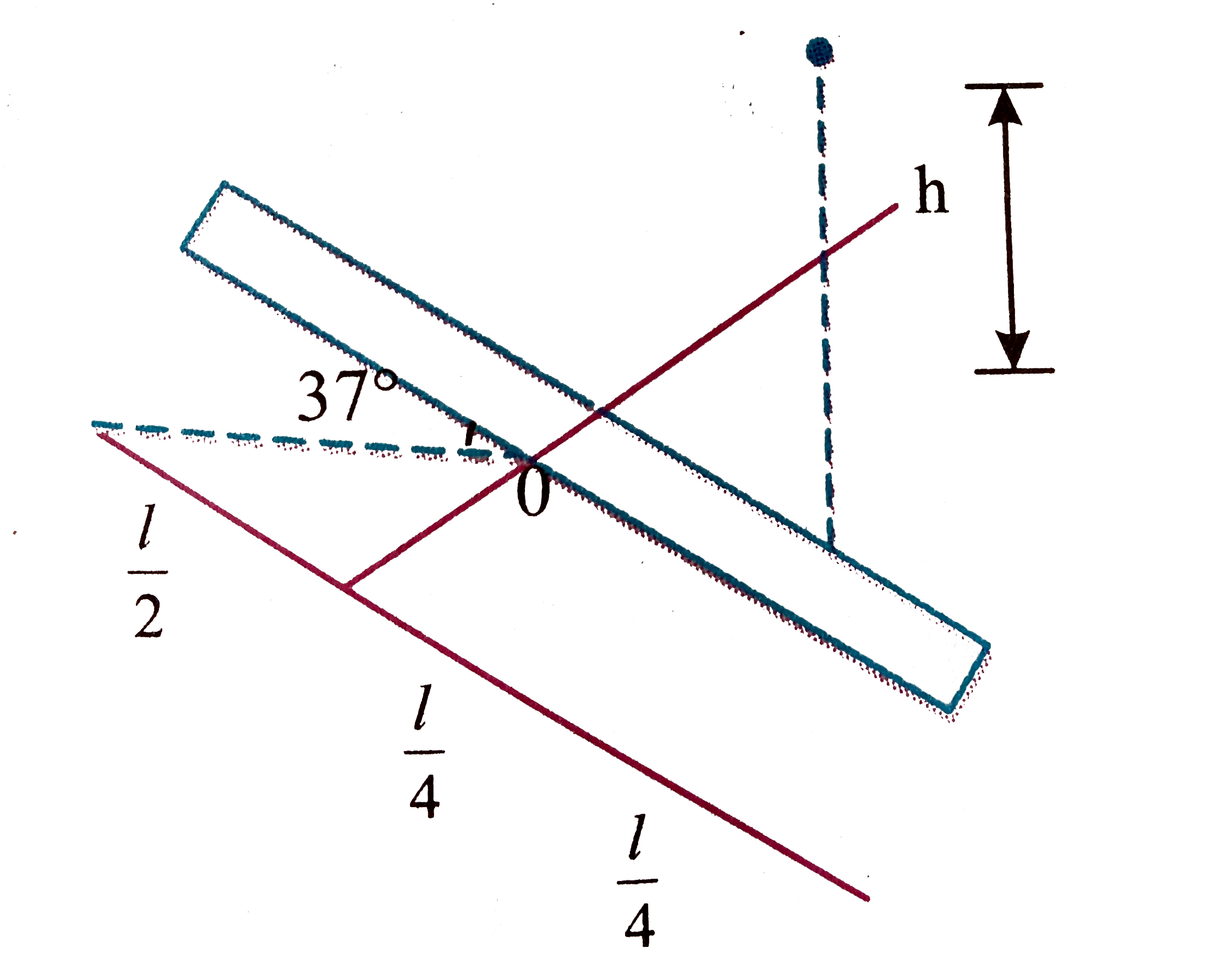
Velocity of particle $P$ after collision $(g = 10 m s^{- 2})$
A $\frac{7}{9} m s^{- 1}$
B $7 m s^{- 1}$
C $\frac{9}{7} m s^{- 1}$
D $1 m s^{- 1}$