A rod of mass m is released on smooth horizontal surface making angle θ with horizontal. Then which of the following statement is correct ?
Acceleration of rod along vertical is less than g
Acceleration of centre of mass along horizontal is zero.
Angular acceleration of rod is not constant
Momentum of the rod along vertical will remain constant
The correct Answer is:D
To solve the problem, we need to analyze the motion of the rod that is released on a smooth horizontal surface at an angle θ with the horizontal.
1. Identify Forces Acting on the Rod:
- The forces acting on the rod include the gravitational force acting downwards (weight mg) and the normal force acting upwards from the surface.
- Since the surface is smooth, there is no friction acting on the rod.
2. Break Down the Gravitational Force:
- The gravitational force can be resolved into two components:
- Vertical component: mgcosθ
- Horizontal component: mgsinθ
3. Apply Newton's Second Law:
- In the vertical direction:
- The normal force N balances the vertical component of the weight:
N=mgcosθ
- Since there is no net force in the vertical direction, the vertical motion does not change, and thus the momentum in the vertical direction remains constant.
- In the horizontal direction:
- The horizontal component of the weight mgsinθ causes acceleration.
- The net force in the horizontal direction is given by:
Fnet=max=mgsinθ
- Therefore, the horizontal acceleration ax can be calculated as:
ax=gsinθ
4. Determine the Angular Motion:
- The rod is not rotating; it is simply translating along the surface.
- The angle θ remains constant, which means there is no angular acceleration:
α=0
5. Conclusion:
- The correct statement regarding the motion of the rod is that the linear momentum in the vertical direction is constant, and the angular acceleration is zero.
Final Answer:
The correct statement is that the linear momentum in the vertical direction is constant, and the angular acceleration of the rod is zero.
- The forces acting on the rod include the gravitational force acting downwards (weight mg) and the normal force acting upwards from the surface.
- Since the surface is smooth, there is no friction acting on the rod.
- The gravitational force can be resolved into two components:
- Vertical component: mgcosθ
- Horizontal component: mgsinθ
- In the vertical direction:
- The normal force N balances the vertical component of the weight:
N=mgcosθ
- Since there is no net force in the vertical direction, the vertical motion does not change, and thus the momentum in the vertical direction remains constant.
- The horizontal component of the weight mgsinθ causes acceleration.
- The net force in the horizontal direction is given by:
Fnet=max=mgsinθ
- Therefore, the horizontal acceleration ax can be calculated as:
ax=gsinθ
- The rod is not rotating; it is simply translating along the surface.
- The angle θ remains constant, which means there is no angular acceleration:
α=0
- The correct statement regarding the motion of the rod is that the linear momentum in the vertical direction is constant, and the angular acceleration is zero.
The correct statement is that the linear momentum in the vertical direction is constant, and the angular acceleration of the rod is zero.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II
16 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - III
1 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
A particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

View SolutionA stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle θ with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
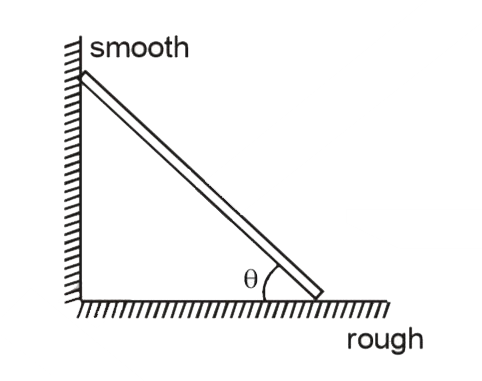
View Solution
Knowledge Check
A particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCPeriod T=2π√lcosθgDCentripetal acceleration a=Fsinθm where F is tensionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.
 AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)A particle of mass m suspended by a string of length l revolves in a horizontal circle such that θ is the angle which the string makes with vertical. Which of the following statement (s) is/are correct ?
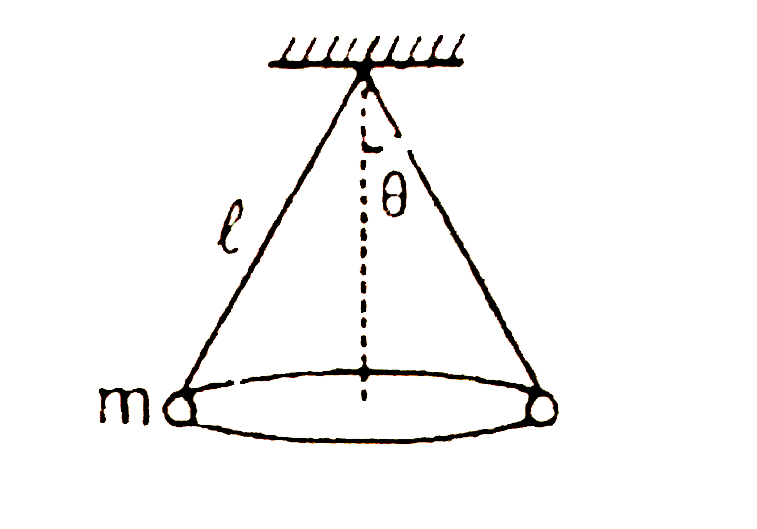 ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCTime period of revolution =2π√lcosθgDCentripetal acceleration =gtanθ
ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCTime period of revolution =2π√lcosθgDCentripetal acceleration =gtanθ
A smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View SolutionA uniform rod of length 2a is held with one end resting on a smooth horizontal table making an angle a with the vertical. Show that when the rod is released, its angular velocity when it makes an angle θ with the vertical is given by
ω=[6g(cosα−cosθ)(1+3sin2α)]
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA homogeneous rod of mass 3 kg is pushed along the smooth horizontal surface by a horizontal suface by a horizontal force F equal to 40 N. The angle θ for which rod hasd pure translation motion is (g=10m/s2)
View SolutionA block of mass m is on the smooth horizontal surface of a plank of mass M The plank is on smooth horizontal surface Now, a constant horizontal force F acts on M. Now, for a person standing on the ground:

View Solution
