Four identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
the x-axis is 23ml2
the z-axis is 43ml2
an axis parallel to the z-axis and passing through a corner is 116ml2
one side is 53ml2
The correct Answer is:A, B, C, D
Step by step video, text & image solution for Four identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - III1videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - IV2videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - I41videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type6videos
PHYSICS PART2
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
Similar Questions
Four identical rods, each of mass m and length l, make a square frame in the xy plane as shown in Fig.
a. Calculate its moment of inertia about the x-and y-axes.
b. Also, calculate its moment of inertia about the z-axis.
 View Solution
View SolutionThree identical rods each of mass M, length l are joined to form an equilateral ΔABC . Find the Moment of Inertia about BC as shown.
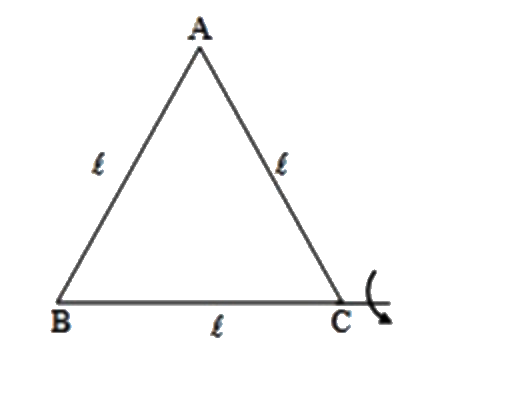 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four charges of 1mC,2mC,3mC and −6mC are placed one at each corner of the square of side 1m.The square lies in the x−y plane with its centre at the origin
AThe electric potential is zero at the originBthe electric potential is zero everywhere along the x-axis only on the sides of the square which are parallel to y-axisCthe electric potential is zero everywhere along the z-axis for any oritentation of the square in the x-y plane.DThe electric potential is not zero along the z-axis except at the origin - Question 2 - Select One
Four identical thin rods each of mass M and length l3, form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is---
A13ml2B43Ml2C23Ml2D133Ml2 - Question 3 - Select One
Four identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
A13Ml2B43Ml2C23Ml2D133Ml2
A uniform rectangular plate has side length l and 2l. The plate is in x−y plane with its centre at origin and sides parallel to x and y axes. The moment of inertia of the plate about an axis passing through a vertex (say A) perpendicular to the plane of the figure is I0. Now the axis is shifted parallel to itself so that moment of inertia about it still remains I0. Write the locus of point of intersection of the axis with xy plane
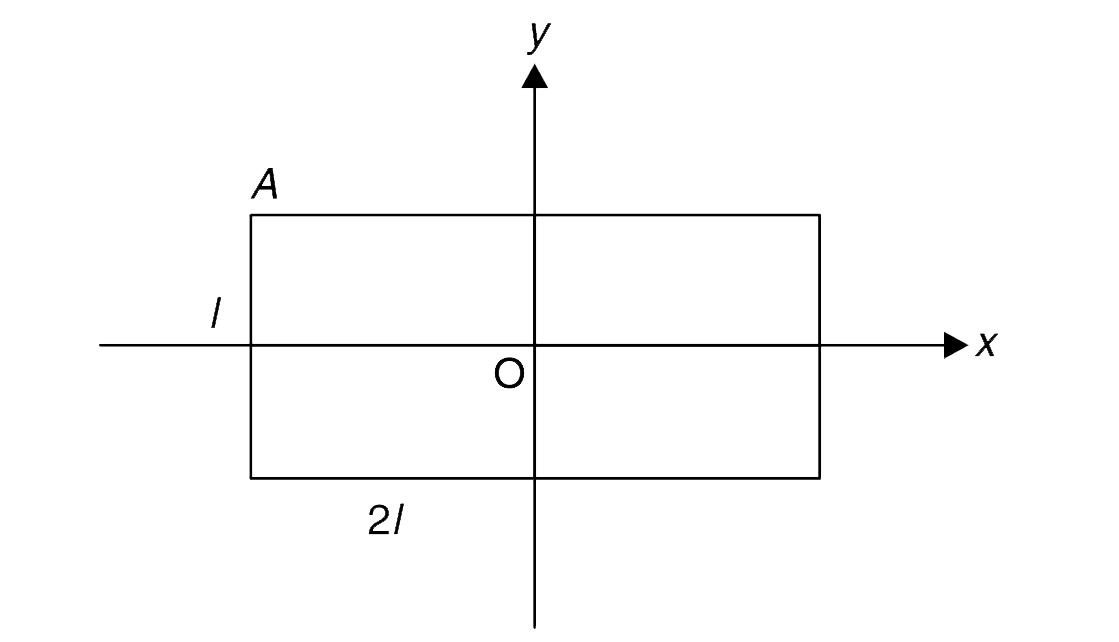 View Solution
View SolutionThree identical thin rods, each of mass m and length l, are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to tis one side and passing through the opposite vertex. Also find its radius of gyration about the given axis.
View SolutionFor identical rods each of mass m and length l make a square frame in xy plane as shown. Calculate its momen of inertia about the x-axis.
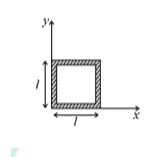 View Solution
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is
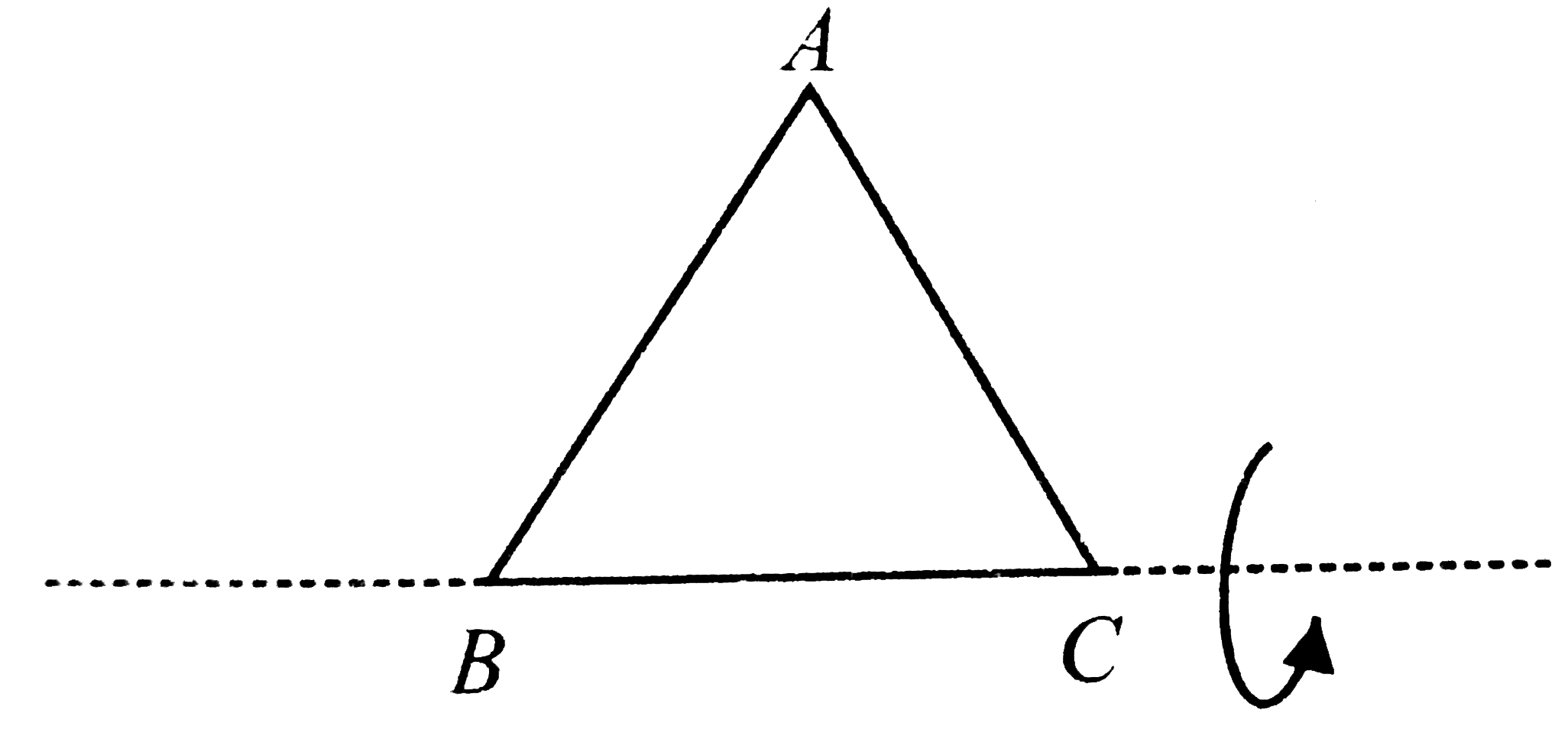 View Solution
View SolutionFour identical solid spheres each of mass M and radius R are fixed at four corners of a light square frame of side length 4R such that centres of spheres coincides with corners of square. The moment of inertia of 4 spheres about an axis perpendicular to the plane to frame and passing through its centre is
View Solution

