A wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
T = 1 . 0 sec and find .
Plot the shape of the string at t = 6 sec.
The wave equation may be written as
Comparing it with the general equation
, we get , =6 cm/sec
(b) The wave equation may be written as
Putting x=0 in the given equation
(c ) The wave equation may be written as
Putting t= 0 in the given equation
(d) 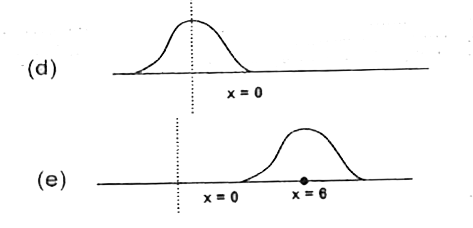
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Solved Problems27videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Comprehension16videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -43videos
CURRENT ELECTRICITY
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.View SolutionA wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.View Solution
Knowledge Check
- Question 1 - Select One
A wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png) Aϕ=0Bϕ≡πCϕ=π/2Dϕ=3π/2
Aϕ=0Bϕ≡πCϕ=π/2Dϕ=3π/2 - Question 2 - Select One or More
A transverse wave travelling on a stretched string is is represented by the equation
y=2(2x−6.2t)2+20. Then ,Avelocity of the wave is 3.1m/sBamplitude of the wave is 0.1mCfrequency of the wave is 20HzDwavelength of the wave is 1m - Question 3 - Select One
Two waves are passing through a region in the same direction at the same time . If the equation of these waves are
y1=asin(2π)λ(vt−x)
and y2=bsin(2π)λ[(vt−x)+x0]
then the amplitude of the resulting wave for x0=(λ/2) isA|a−b|Ba+bC√a2+b2D√a2+b2+2abcosx
A wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by
y=Ae(−tt−xA)2
where A=5mm, T=1.0 s and λ=8.0cm
(a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 sView SolutionA wave pulse is travelling on a string at 2m/s along positive x-directrion. Displacement y of the particle at x = 0 at any time t is given by
y=2t2+1 Find
Shape of the pulse at t = 0 and t = 1s.View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?View SolutionA wave propagates on a string in the positive x-direction at a velocity u. The shape of the string at t=t0 is given by g(x,t0)=Asin(xa) . Write the wave equation for a general time t.
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given byView Solution

