State whether the following functions can represent wave motion ?
y=√(x−vt)
y=(x−vt)2
y=A(x−vt)
y=Alog(x+vt)3
To determine whether the given functions can represent wave motion, we need to analyze each function based on the criteria for wave motion. A function representing wave motion must be continuous, single-valued, harmonic, and finite at every point.
1. Analyze Option 1: y=√1+x
- Substitute x=1 and t=0:
y=√1+1=√2
- The function y=√1+x gives two values for certain inputs (e.g., y=√1+x can yield both positive and negative roots). Therefore, it is not single-valued.
- Conclusion: Option 1 does not represent wave motion.
2. Analyze Option 2: y=x−vt2
- This function is a polynomial and does not have the form of sine or cosine, which are necessary for harmonic functions.
- Since it does not meet the harmonic criterion, it cannot represent wave motion.
- Conclusion: Option 2 does not represent wave motion.
3. Analyze Option 3: y=e−x2
- This function is continuous and single-valued. However, it does not have the form of a sine or cosine function, which is required for harmonic functions.
- Conclusion: Option 3 does not represent wave motion.
4. Analyze Option 4: y=1x+t
- Substitute x=0 and t=0:
y=10+0(undefined)
- The function is not defined when x+t=0, indicating it is not finite at every point.
- Conclusion: Option 4 does not represent wave motion.
Final Conclusion:
None of the given options represent wave motion as they do not satisfy the necessary criteria of being continuous, single-valued, harmonic, and finite at every point.
- Substitute x=1 and t=0:
y=√1+1=√2
- The function y=√1+x gives two values for certain inputs (e.g., y=√1+x can yield both positive and negative roots). Therefore, it is not single-valued.
- Conclusion: Option 1 does not represent wave motion.
- This function is a polynomial and does not have the form of sine or cosine, which are necessary for harmonic functions.
- Since it does not meet the harmonic criterion, it cannot represent wave motion.
- Conclusion: Option 2 does not represent wave motion.
- This function is continuous and single-valued. However, it does not have the form of a sine or cosine function, which is required for harmonic functions.
- Conclusion: Option 3 does not represent wave motion.
- Substitute x=0 and t=0:
y=10+0(undefined)
- The function is not defined when x+t=0, indicating it is not finite at every point.
- Conclusion: Option 4 does not represent wave motion.
None of the given options represent wave motion as they do not satisfy the necessary criteria of being continuous, single-valued, harmonic, and finite at every point.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Exercise 31videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Exercise 41videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Exercise 11videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -43videos
CURRENT ELECTRICITY
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following equations represents a wave ?
Ay=Asinωt,By=Acoskx,Cy=Asin(at−bx+c)Dy=A(ωt−kx) - Question 2 - Select One
Which of the following equations represents a wave
AY=A(ωt−kx)BY=AcoskxCY=AsinωtDY=Asin(at−bx+c) - Question 3 - Select One
State whether the following statements is false ?
A√23 is a rational number.BThere are infinitely many rational between any two integers.CNumber of rational numbers between 15 and 18 is infinite.DRational are numbers which can be written in the form pq , q≠0, p and q both are integers.
State whether the following is not the probability mass function of random variable. Give reasons for your answer.
 View Solution
View SolutionWhich of the following functions of time represent periodic motion ?
View SolutionWhich of the following is an example of transverse wave motion ?
View SolutionWhich of the following functions represent a stationary wave ? Here a,b and c are constants:
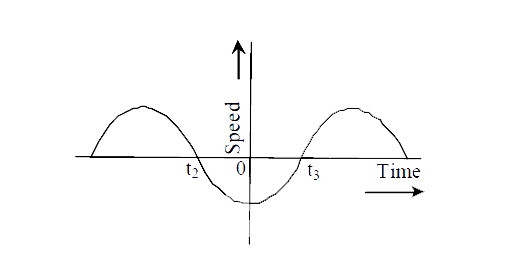
View SolutionState whether the following graph can be seen in nature or not. Explain.
 View Solution
View Solution