The trajectory of a body with two simultaneous, mutually perpendicular oscillations is determined by
where x and y are the projections of the body displacement on X and Y axes
For simplicity, assume . Then, the equation of trajectory will be
which is a general equation of ellipse.
But if , then the graph of trajectory on the X-Y plane is either a closed curve, whose loop number is defined by the ratio n = p/q, or an open curve.
Note that at the point where the curve reverses along the same trajectory, the velocities along the X-axis and Y-axis become equal to zero simultaneously. The body moving along the curve stops exactly at this moment at a certain point, say P, and then starts moving back,
The closed curve for the motion of the body with the above two oscillations (1) and (2) with certain values of p, q and is given in the adjacent figure. The value of p/q is
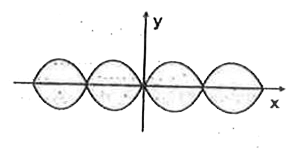
The correct Answer is:C
Topper's Solved these Questions
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assertion Reasoning
1 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Numerical
6 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Solved Problems
27 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
A particle simultaneously participates in two mutually perpendicular oscillations x=sinπt & y=2cos2πt. Write the equation of trajectory of the particle.
View SolutionA particle simultaneously participates in two mutually perpendicular oscillations x=sinπt & y=2cos2πt. Write the equation of trajectory of the particle.
View Solution
Knowledge Check
The trajectory of a body with two simultaneous, mutually perpendicular oscillations is determined by
x=asin(pωt) (1)
y=bsin(qωt+ϕ) (2)
where x and y are the projections of the body displacement on X and Y axes
For simplicity, assume pω=qω=ω0. Then, the equation of trajectory will be
y2b2+x2a2−2xyabcosϕ=sin2ϕ (3)
which is a general equation of ellipse.
But if qω≠pωandp≠q, then the graph of trajectory on the X-Y plane is either a closed curve, whose loop number is defined by the ratio n = p/q, or an open curve.
Note that at the point where the curve reverses along the same trajectory, the velocities along the X-axis and Y-axis become equal to zero simultaneously. The body moving along the curve stops exactly at this moment at a certain point, say P, and then starts moving back,
If p = 2, q = 1 and ϕ=0, the path of trajectory of motion of the body with the above two oscillations (1) and (2) isAan ellipseBa parabolaCa straight lineDnone of the aboveA particle simultaneously participates in two mutually perpendicular oscillations , x=2 sin ωt , y =2 cos ω t . The trajectory of motion will be
Aa straight lineBa parabolaCa circleDnone of theseThe trajectories orhtogonal to x2+y2=2ax is
Ay=x2By=C(x2+y2)Cy=C(x2+2y2)Dy2=Cx
The equation of trajectory of an oblique projectile y=√3x−gx22. The angle of projection is
View SolutionEquation for two waves is given as y1=asin(ωt+ϕ1),y2=asin(ωt+ϕ2).
If ampitude and time period of resultant wave does not change, then calculate (ϕ1−ϕ2).
View SolutionEquation for two waves is given as y1=asin(ωt+ϕ1),y2=asin(ωt+ϕ2).
If ampitude and time period of resultant wave does not change, then calculate (ϕ1−ϕ2).
View SolutionThe equation of trajectory of an oblique projectile y=√3x−gx22. The angle of projection is
View SolutionThe trajectories orthogonal to (2a−x)y2=x2 is
View Solution
