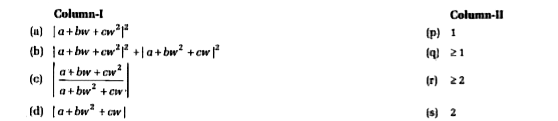If $a, b, c$ are integers not all equal and w is a cube root of unity $(w \neq 1)$ , then the minimum value of $∣ ∣ a + b w + c w^{2} ∣ ∣$ is

A

$0$

B

$1$

C

$1 / 2 < | z | < 3 / 4$

D

$1 / 2$

Text Solution

Verified by Experts

The correct Answer is:B

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBER

Topper's Solved these Questions

BOOK - FIITJEECHAPTER - COMPLEX NUMBEREXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II
22videos
COMPLEX NUMBER
BOOK - FIITJEECHAPTER - COMPLEX NUMBEREXERCISE - COMPREHENSION - I
3videos
COMPLEX NUMBER
BOOK - FIITJEECHAPTER - COMPLEX NUMBEREXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II
10videos
COMPLEX NUMBER
BOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Numerical Based
2videos
CIRCLE
BOOK - FIITJEECHAPTER - DEFINITE INTEGRAL EXERCISE - NUMERICAL BASED
3videos
DEFINITE INTEGRAL

Similar Questions

Knowledge Check

Question 1 - Select One
. If a b, and c are integers not all equal and $ω$ is a cube root of unity (where $ω \neq 1$ ), then minimum value of ${∣ ∣ a + b ω + c ω^{2} ∣ ∣}^{2}$ is equal to
A0
B1
C $\frac{\sqrt{3}}{2}$
D $\frac{1}{2}$
Question 2 - Select One
If a,b,c are distinct integers and $ω (\neq 1)$ is a cube root of unity, then the minimum value of $∣ ∣ a + b ω + c ω^{2} ∣ ∣ + ∣ ∣ a + b ω^{2} + c ω ∣ ∣$ is
A2
B3
C $4 \sqrt{2}$
D $6 \sqrt{2}$
Question 3 - Select One
If a,b,c are distinct integers and $ω (\neq 1)$ is a cube root of unity, then the minimum value of $∣ ∣ a + b ω + c ω^{2} ∣ ∣ + ∣ ∣ a + b ω^{2} + c ω ∣ ∣$ is
A $2 \sqrt{3}$
B3
C $4 \sqrt{2}$
D2

FIITJEE-COMPLEX NUMBER-ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I

Home
Ask Doubt
Profile