Let X and Y be two variables with correlation coefficient e. If the values of X and Y serires and changed such that the cov (X,Y) remains unchanged while the variance of X and Y becomes 4 times their original values, then find the new correlation coefficient between X and Y.
The correct Answer is:e/4
To find the new correlation coefficient between X and Y after the changes in their variances, we can follow these steps:
Step 1: Understand the correlation coefficient formula
The correlation coefficient r between two variables X and Y is given by the formula:
rX,Y=Cov(X,Y)√Var(X)⋅Var(Y)
Where:
- Cov(X,Y) is the covariance between X and Y.
- Var(X) is the variance of X.
- Var(Y) is the variance of Y.
Step 2: Define the initial conditions
Let:
- The initial correlation coefficient be e.
- The initial covariance be Cov(X,Y).
- The initial variances be Var(X) and Var(Y).
From the formula, we can express the initial correlation as:
e=Cov(X,Y)√Var(X)⋅Var(Y)
Step 3: Analyze the changes
According to the problem:
- The covariance Cov(X,Y) remains unchanged.
- The variances of X and Y become 4 times their original values:
- New variance of X: Var(X)new=4⋅Var(X)
- New variance of Y: Var(Y)new=4⋅Var(Y)
Step 4: Substitute into the correlation formula
Now, we can find the new correlation coefficient rnew:
rnew=Cov(X,Y)√Var(X)new⋅Var(Y)new
Substituting the new variances:
rnew=Cov(X,Y)√(4⋅Var(X))⋅(4⋅Var(Y))
rnew=Cov(X,Y)√16⋅Var(X)⋅Var(Y)
rnew=Cov(X,Y)4⋅√Var(X)⋅Var(Y)
Step 5: Relate the new correlation to the old correlation
From our initial correlation e:
rnew=14⋅Cov(X,Y)√Var(X)⋅Var(Y)
Thus,
rnew=e4
Final Answer
The new correlation coefficient between X and Y is:
e4
The correlation coefficient r between two variables X and Y is given by the formula:
rX,Y=Cov(X,Y)√Var(X)⋅Var(Y)
Where:
- Cov(X,Y) is the covariance between X and Y.
- Var(X) is the variance of X.
- Var(Y) is the variance of Y.
Let:
- The initial correlation coefficient be e.
- The initial covariance be Cov(X,Y).
- The initial variances be Var(X) and Var(Y).
e=Cov(X,Y)√Var(X)⋅Var(Y)
According to the problem:
- The covariance Cov(X,Y) remains unchanged.
- The variances of X and Y become 4 times their original values:
- New variance of X: Var(X)new=4⋅Var(X)
- New variance of Y: Var(Y)new=4⋅Var(Y)
Now, we can find the new correlation coefficient rnew:
rnew=Cov(X,Y)√Var(X)new⋅Var(Y)new
Substituting the new variances:
rnew=Cov(X,Y)√(4⋅Var(X))⋅(4⋅Var(Y))
rnew=Cov(X,Y)√16⋅Var(X)⋅Var(Y)
rnew=Cov(X,Y)4⋅√Var(X)⋅Var(Y)
From our initial correlation e:
rnew=14⋅Cov(X,Y)√Var(X)⋅Var(Y)
Thus,
rnew=e4
The new correlation coefficient between X and Y is:
e4
Topper's Solved these Questions
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Assignment Problems (Objective) Level -I
20 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Assignment Problems (Objective) Level II
25 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Exercise 3
2 Videos
- SET, RELATION & FUNCTIONBOOK - FIITJEECHAPTER - SET, RELATION & FUNCTIONEXERCISE - Exercise 3
8 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED
4 Videos
Similar Questions
Knowledge Check
Correlation coefficient r of two variables X and Y is positive when
AσX+Y>σX−YBσX−Y>σX+YCσX+Y=0Dnone of theseThe correlation between two variables x and y is given to be r. The values of x and y change such that cov (x, y) remains unaltered and var (x) and var (y) are changed to four times their original values. The new correlation coefficient is changed to
A4rB16rCr/16Dr/4if the regression coefficient of Y on X is4/3,then the regression coefficient of X and Y :
A−1/4B1/4C−1/2D1/2
Calculate the coeficient of correlation between X and Y.
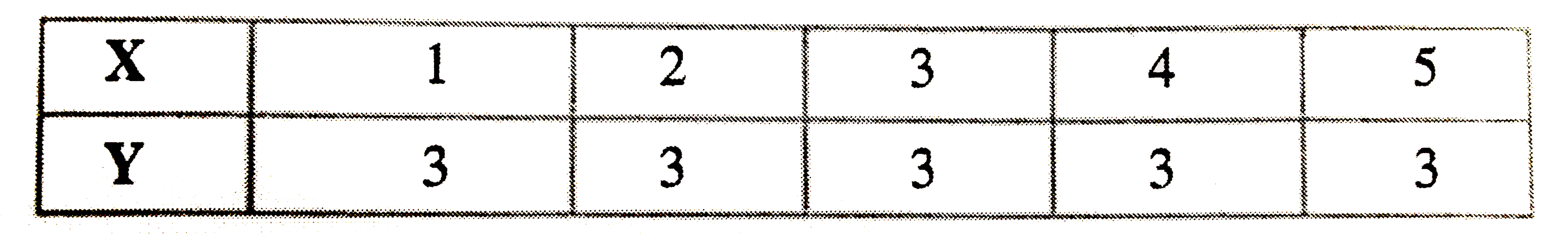
View SolutionIf the correlation coefficient between the random variables X and Y is negative, then E(XY)>E(X)E(Y)
View SolutionCalculate coefficient of correlation between series X and Y.

View SolutionIf the regression coefficients of X on Y and Y on X are −0.4,and−0.9 respectively, then the correlation coefficient between X and Y is …………
View SolutionIf two variables X and Y are independent, then what is correlation coefficient between them
View Solution

