Let 5x+3y=55 and 7x+y=45 be two lines of regression for a bivariate data
Coefficient of correlation between x and y
√521
−√521
√215
−√215
The correct Answer is:B
To find the coefficient of correlation r between x and y given the lines of regression 5x+3y=55 and 7x+y=45, we can follow these steps:
Step 1: Rearranging the equations to find the regression coefficients
1. First Line of Regression:
5x+3y=55
Rearranging for y:
3y=55−5x⟹y=−53x+553
The coefficient of x here is byx=−53.
2. Second Line of Regression:
7x+y=45
Rearranging for y:
y=45−7x
The coefficient of x here is bxy=−7.
Step 2: Finding the product of the regression coefficients
Now, we can find the product of the regression coefficients:
byx⋅bxy=(−53)⋅(−7)=5⋅73=353
Step 3: Relating the product to the coefficient of correlation
The relationship between the regression coefficients and the coefficient of correlation r is given by:
byx⋅bxy=r2
Thus,
r2=353
Step 4: Finding the value of r
To find r, we take the square root of r2:
r=√353
Step 5: Determining the sign of r
Since both regression coefficients byx and bxy are negative, the correlation will be negative:
r=−√353
Final Answer
The coefficient of correlation r between x and y is:
r=−√353
---
5x+3y=55
Rearranging for y:
3y=55−5x⟹y=−53x+553
The coefficient of x here is byx=−53.
7x+y=45
Rearranging for y:
y=45−7x
The coefficient of x here is bxy=−7.
byx⋅bxy=(−53)⋅(−7)=5⋅73=353
byx⋅bxy=r2
Thus,
r2=353
r=√353
r=−√353
r=−√353
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Assertion -Reasoning Type MCQ Single Correct(Level II)2videos
STATISTICS
- BOOK - FIITJEECHAPTER - SET, RELATION & FUNCTIONEXERCISE - Exercise 38videos
SET, RELATION & FUNCTION
- BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED4videos
STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
Let 5x+3y=55 and 7x+y=45 be two lines of regression for a bivariate data
The Acute angle between the two lines of regression isAtan−1(1918)Btan−1(1613)Ctan−1(1316)Dtan−1(819) - Question 2 - Select One
The coefficient of correlation between X and Y is 0.6 U and V are two variables defined as U=x−32,V=y−23, then the coefficient of correlation between U and V is
A0.1B0.3C0.2D1
Find the Kari Pearson's Coefficient of correlation between x and y for the data
 View Solution
View SolutionAngle between lines of regression of the variables x and y with coefficient of correlation r is …………….
View SolutionIf the two lines of regression are 3x+2y=26and6x+y=31, then the coefficient of correlation between x and y is ……………..
View SolutionFind (i) mean →xand→y, (ii) regression coefficeint byxandbxy, (iii) coefficeint of correlation between x and y for the following two regression lines 2x+3y-10=0 and 4x+y-5=0
View SolutionFind the regression coefficient byx and bxy and the two lines of regression for the following data. Also compute the correlation coefficient
View SolutionFrom the following data, determine Karl Pearson's coefficient of correlation between X and Y series for 15 pairs .
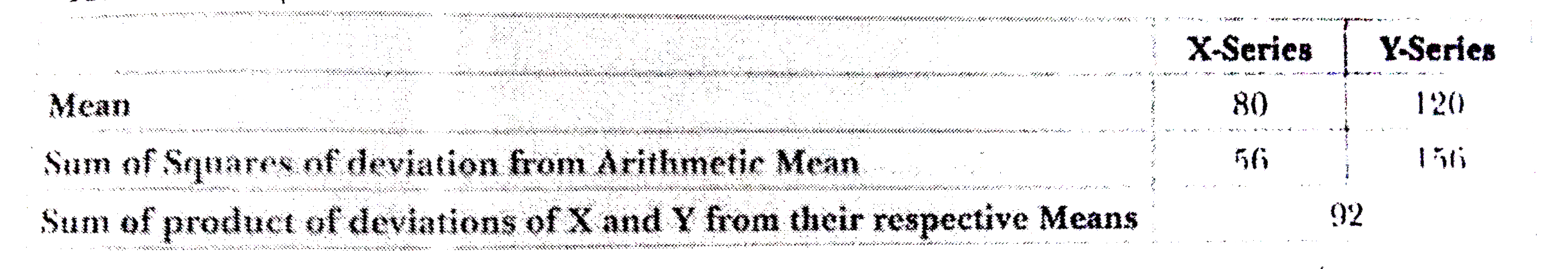 View Solution
View Solution



