The equation α=D−d(n−1)d is correctly matched for
A⇔nB/2=nC/3
A⇔nB/3+(2n/3)C
A→(n/2)B+(n/4)C
A⇔(n/2)B+C
The correct Answer is:B
To solve the equation α=D−d(n−1)d and determine the correct context in which it applies, we need to analyze the terms involved in the equation and the chemical reactions that fit this description.
1. Understanding the Terms:
- α: Degree of dissociation, which indicates the fraction of the reactant that has dissociated into products.
- D: Vapor density before dissociation.
- d: Vapor density after dissociation.
- n: Number of moles of gaseous products formed from 1 mole of reactant.
2. Identifying the Reaction Type:
- The equation is applicable to a reaction where one mole of a reactant dissociates into n moles of products. This is essential for applying the formula correctly.
3. Analyzing the Given Options:
- We need to find a reaction where the reactant is 1 mole and the total number of moles of products is n.
- Let's evaluate the provided equations one by one.
4. Evaluating the First Option:
- Reaction: A⇌n3B+2n3C
- Reactant moles: 1 (for A)
- Product moles: n3+2n3=n
- This fits the criteria, so this option is valid.
5. Evaluating the Second Option:
- Reaction: A⇌n2B+n4C
- Reactant moles: 1 (for A)
- Product moles: n2+n4=3n4
- This does not fit since 3n4≠n.
6. Evaluating the Third Option:
- Reaction: A⇌n3B+2n3C (same as the first option)
- This has already been validated as correct.
7. Evaluating the Fourth Option:
- Reaction: A⇌n2B+C
- Reactant moles: 1 (for A)
- Product moles: n2+1
- This does not fit since n2+1≠n unless n=2, which is not a general case.
8. Conclusion:
- The only valid reaction that fits the equation α=D−d(n−1)d is the first option, where the total number of moles of products equals n when starting from 1 mole of reactant.
Final Answer:
The equation α=D−d(n−1)d is correctly matched for the reaction A⇌n3B+2n3C.
- α: Degree of dissociation, which indicates the fraction of the reactant that has dissociated into products.
- D: Vapor density before dissociation.
- d: Vapor density after dissociation.
- n: Number of moles of gaseous products formed from 1 mole of reactant.
- The equation is applicable to a reaction where one mole of a reactant dissociates into n moles of products. This is essential for applying the formula correctly.
- We need to find a reaction where the reactant is 1 mole and the total number of moles of products is n.
- Let's evaluate the provided equations one by one.
- Reaction: A⇌n3B+2n3C
- Reactant moles: 1 (for A)
- Product moles: n3+2n3=n
- This fits the criteria, so this option is valid.
- Reaction: A⇌n2B+n4C
- Reactant moles: 1 (for A)
- Product moles: n2+n4=3n4
- This does not fit since 3n4≠n.
- Reaction: A⇌n3B+2n3C (same as the first option)
- This has already been validated as correct.
- Reaction: A⇌n2B+C
- Reactant moles: 1 (for A)
- Product moles: n2+1
- This does not fit since n2+1≠n unless n=2, which is not a general case.
- The only valid reaction that fits the equation α=D−d(n−1)d is the first option, where the total number of moles of products equals n when starting from 1 mole of reactant.
The equation α=D−d(n−1)d is correctly matched for the reaction A⇌n3B+2n3C.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE (LEVEL -I) REASONING TYPE QUESTIONS))6videos
CHEMICAL EQUILIBRIUM
- BOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ( LEVEL -II))20videos
CHEMICAL EQUILIBRIUM
- BOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE)3videos
CHEMICAL EQUILIBRIUM
- BOOK - FIITJEECHAPTER - CHEMICAL ENERGETICS EXERCISE - NUMERICAL BASED QUESTIONS2videos
CHEMICAL ENERGETICS
- BOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Exercise9videos
CHEMICAL KINETICS AND RADIOACTIVITY
Similar Questions
Knowledge Check
- Question 1 - Select One
The degree of dissociation (α) can be calculated using the formula,
α=dt−d0(n−1)d0
This formula is applicable atAconstant volume and constant temperatureBconstant volume and variable temperatureCconstant pressure and constant temperatureDall the above conditions - Question 2 - Select One
In the above question, α varies with Dd according to:
A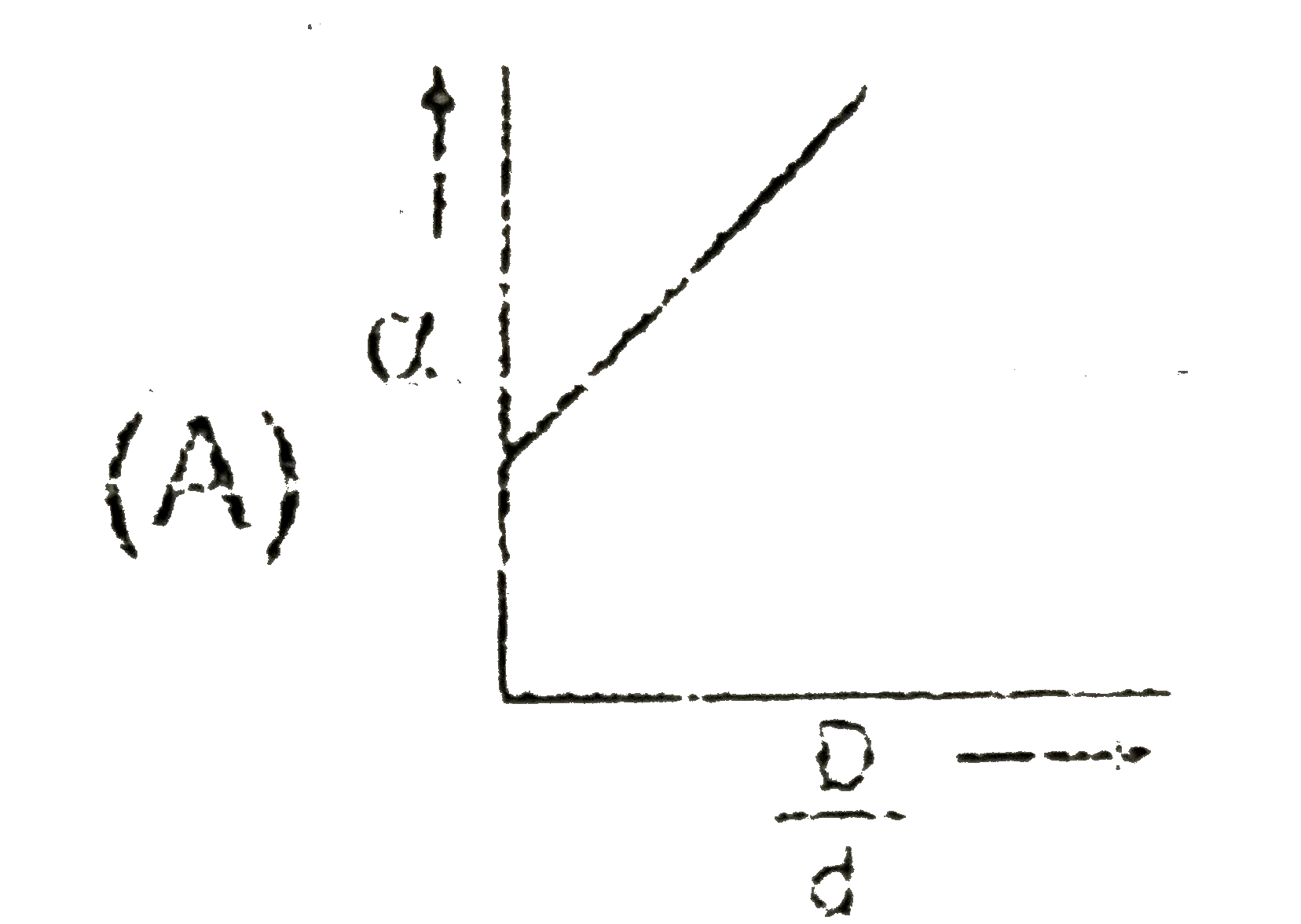 B
B C
C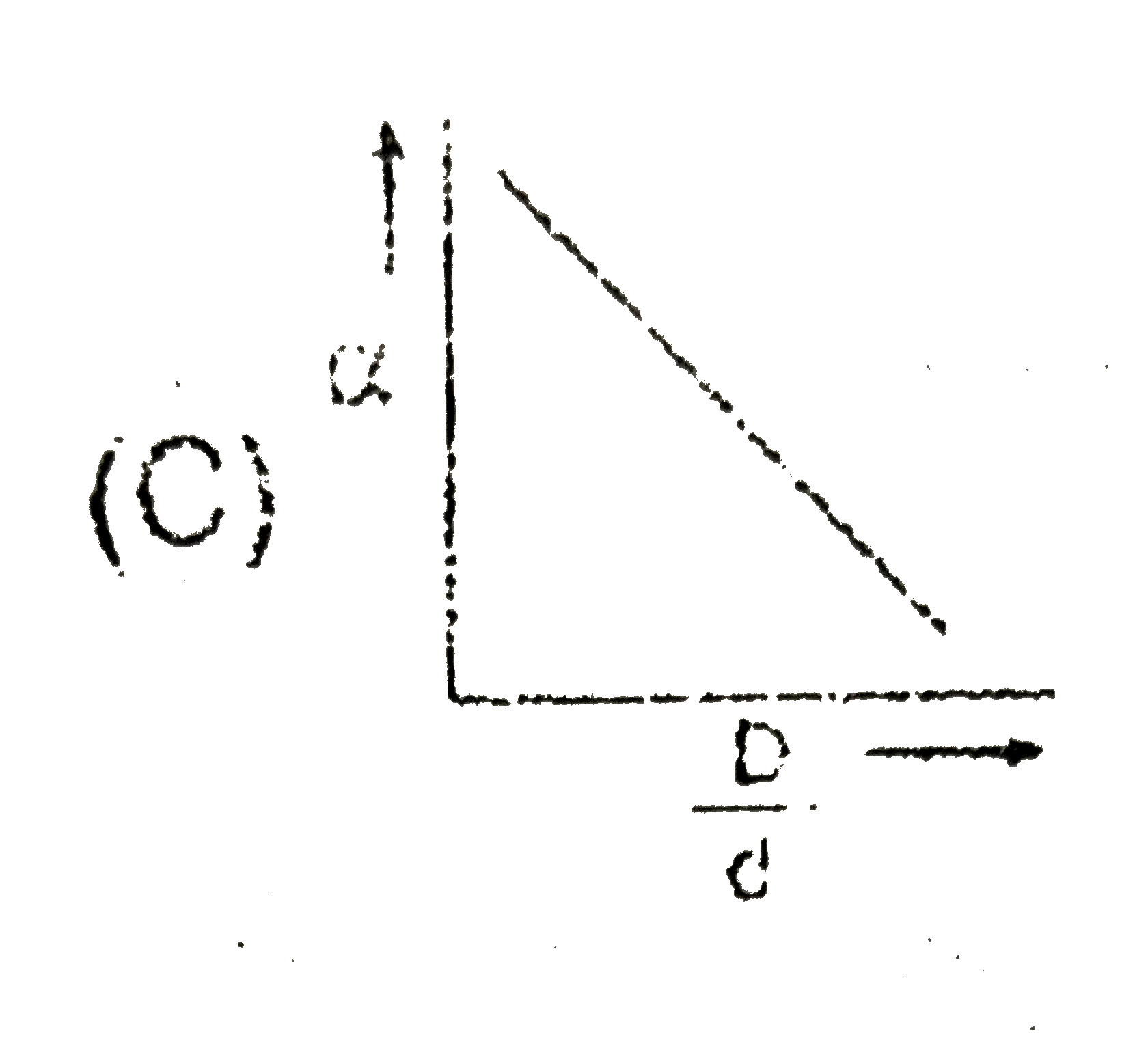 D
D
- Question 3 - Select One
Which of the following pairs are correctly matched ?
(a) 1 and 2
(b) 2 and 3
(c) 1 and 3
(d) 1, 2 and 3A1 and 2B2 and 3C1 and 3D1, 2 and 3
α−D−(+) glucose and β−D−(+) glucose are
View Solutionα-(D)-(-)fructose and β-(D)-(-) fructose are
View Solutionα-(D)-(-)fructose and β-(D)-(-) differs in orientation at
View SolutionIn the formulae Sn=n2{2a+(n−1)d} make d as the subject
The following steps are involved in solving the above problem. Arrange them in sequential order.
(A) (n−1)d=2Snn−2a
(B) Given, Sn=n2[2a+(n−1)d]⇒n[2a+(n−1)d]
=2Sn
(C) ⇒d=2n−1[Snn−a]
(D) 2a+(n−1)d=2SnnView SolutionIn the formulae Sn=n2{2a+(n−1)d} make d as the subject
The following steps are involved in solving the above problem. Arrange them in sequential order.
(A) (n−1)d=2Snn−2a
(B) Given, Sn=n2[2a+(n−1)d]⇒n[2a+(n−1)d]
=2Sn
(C) ⇒d=2n−1[Snn−a]
(D) 2a+(n−1)d=2SnnView Solution

