Energy required to stop the ejection of electrons from Cu plate is 0.24eV. Calculate the work function when radiations of strikes the plate.
The correct Answer is:4.65eV
To solve the problem, we need to calculate the work function of the copper plate when it is struck by radiation of wavelength λ=253.7nm. The energy required to stop the ejection of electrons (the kinetic energy of the ejected electrons) is given as 0.24eV.
1. Convert the Wavelength to Meters:
λ=253.7nm=253.7×10−9m
Hint: Remember that 1nm=10−9m.
2. Calculate the Energy of the Incident Radiation:
The energy E of the radiation can be calculated using the formula:
E=hcλ
where:
- h=6.63×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
Substituting the values:
E=(6.63×10−34J s)×(3×108m/s)253.7×10−9m
Calculating this gives:
E≈7.83×10−19J
Hint: Make sure to keep track of units when substituting values into the formula.
3. Convert Energy from Joules to Electron Volts:
To convert the energy from Joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
E≈7.83×10−19J1.6×10−19J/eV≈4.89eV
Hint: Always remember to use the conversion factor correctly to avoid calculation errors.
4. Calculate the Work Function:
The work function ϕ can be calculated using the equation:
E=ϕ+KE
where KE is the kinetic energy of the ejected electrons. Rearranging gives:
ϕ=E−KE
Substituting the values:
ϕ=4.89eV−0.24eV=4.65eV
Hint: Ensure that you are subtracting the kinetic energy from the total energy correctly.
Final Answer:
The work function of the copper plate is approximately 4.65eV.
λ=253.7nm=253.7×10−9m
The energy E of the radiation can be calculated using the formula:
E=hcλ
where:
- h=6.63×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
E=(6.63×10−34J s)×(3×108m/s)253.7×10−9m
E≈7.83×10−19J
To convert the energy from Joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
E≈7.83×10−19J1.6×10−19J/eV≈4.89eV
The work function ϕ can be calculated using the equation:
E=ϕ+KE
where KE is the kinetic energy of the ejected electrons. Rearranging gives:
ϕ=E−KE
Substituting the values:
ϕ=4.89eV−0.24eV=4.65eV
The work function of the copper plate is approximately 4.65eV.
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - FIITJEECHAPTER - ATOMIC STRUCTUREEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I
10 Videos
- ATOMIC STRUCTUREBOOK - FIITJEECHAPTER - ATOMIC STRUCTUREEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL II
14 Videos
- ATOMIC STRUCTUREBOOK - FIITJEECHAPTER - ATOMIC STRUCTUREEXERCISE - REASONING TYPE QUESTIONS
14 Videos
- ALKYL AND ARYL HALIDESBOOK - FIITJEECHAPTER - ALKYL AND ARYL HALIDESEXERCISE - NUMERICAL BASED QUESTIONS
1 Videos
- CARBOHYDRATES, AMINO ACIDS, POLYMERS AND PRACTICAL ORGANIC CHEMISTRYBOOK - FIITJEECHAPTER - CARBOHYDRATES, AMINO ACIDS, POLYMERS AND PRACTICAL ORGANIC CHEMISTRYEXERCISE - EXERCISE
4 Videos
Similar Questions
The energy required to stop ejection of electrons from a Cu plate is 0.24eV .Calculate the work function Cu when a radiation of wavelength λ=250 nm strikes the plate
View Solution0.24eV of energy is required to stop photoelectron emitted by radiation of wavelength 2480Å. Find work function of metal used?
View Solution
Knowledge Check
Energy required to stop the ejection of electrons from certain metal plate was found to be 0.2 eV when an electromagnetic radiation of 330 nm was made to fall on it the work function of the metal is
A0.32×10−19 jB6×10−19jC5.68×10−19 jD3.82×10−27The wavelength of the electron emitted by a metal sheet of work function 5 eV when photons from EMR of wavelength 62 nm strike the metal plate .
A82.667ÅB3.16 nmC0.316 nmD826.67ÅThe wavelength of the electron emitted by a metal sheet of work function 5eV when photons from EMR of wavelength 62 nm strike the metal plate
A82.667 ÅB3.16 nmC0.316 nmD826.67Å
The mercury line of wavelength 2356Å is used to eject photoelectrons from silver. The difference in potentials required to bring the electrons to rest is 0.11 eV. Calculate the energy in electron volts necessary to remove an electron from silver.
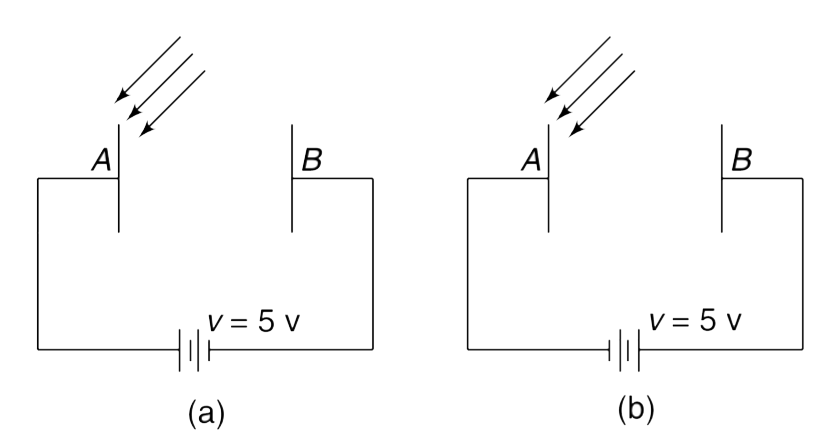
View SolutionIn a photoelectric experiment, a monochromatic light is incident on the metal plate A. It was observed that with V=5volt, the maximum kinetic energy of photoelectrons striking plate B was 1eV. The polarity of the applied potential difference was as shown in figure (a). With polarity of the applied potential difference reversed (as shown in figure (b)) and frequency of incident light doubled, it was observed that in saturation state, the kinetic energy of electrons striking plate B ranged between 5 eV to 20 eV. Find the work function of metal used in plate A.
View SolutionWhat amount of energy sould be added to an electron to reduce its de Broglie wavelength λ1=550nm incident on it, causing the ejection of photoelectrons for which the stopping potential is Vs1=0.19V. If the radiation of wavelength λ2=190nm is now incident on the surface, (a) calculate the stopping potential VS2, (b) the work function of the surface, and (c) the threshold frequency for the surface.
View SolutionIf threshold wavelength (λ0) for ejection of electron from metal is 330 nm, then work function for the photoelectron emission is
View SolutionIf the threshold wavelength (λ0) for ejection of electron from metal is 330 nm, then work function for the photoelectric emission is:
View Solution
