In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
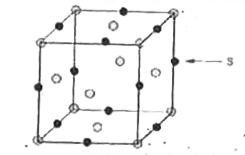
tetrahedral void
cubic void
octahedral void
None of the above
The correct Answer is:C
Topper's Solved these Questions
- SOLID STATEBook:FIITJEEChapter:SOLID STATEExercise:(COMPREHENSION - II)
Explore 4 Videos
- SOLID STATEBook:FIITJEEChapter:SOLID STATEExercise:(COMPREHENSION - IV)
Explore 2 Videos
- SOLID STATEBook:FIITJEEChapter:SOLID STATEExercise:(REASONING TYPE QUESTIONS)
Explore 1 Video
- QUALITATIVE ANALYSIS Book:FIITJEEChapter:QUALITATIVE ANALYSIS Exercise:Single interger answer type
Explore 3 Videos
- STOICHIOMETRY AND BALANCING REDOX REACTION Book:FIITJEEChapter:STOICHIOMETRY AND BALANCING REDOX REACTION Exercise:SINGLE INTEGER ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
Defects which do not disturb the stoichiometry are called stochiometric defect. At the time of crystal formation an ion may not occupy its expected position leaving a void or hole at that site. As a metter of fact one positive and one negative ion are missing from their respective positions leaving behind a pair of holes. This vacancy is a Schottky defect. Due to this defect density decreases. Defect arises in which certain atoms or ions have migrated to interstitial position some distance removed from the holes which they vacated. In this case there is no change in the density of the crystal.
In stoichiometric defects, the ratio of positive and negative ions as indicated by chemical formula of the compound
View SolutionX-ray crystallography reveals many aspects of the structure of metal halldes. The radius ratio (r+/r−) is a useful parameter to rationalize their structure and stability. A table or radius ratio (r+/r−) for some alkali halide is given below :


For a given anion, the graph for NaCl type structure levels off at low r+/r− values because of :
View SolutionStatement I: In any ionic solid [MX] with Schottky defect, the number of positive and negative ions are same.
Statement II: An equal number of cation and anion vacancies is present.
View SolutionNumber of oxygen atoms in molybdate ion is
View SolutionIn the following reaction we start with 2 mol of N2 and 5 of H2 exerting a total pressure of 7 atm at a given temperature in a closed vessel when 50% of N2 is converted into NH3,N2+3H2→2NH3
What will be the partial pressure of NH3 in atmosphere ?
View SolutionAssertion : In hexagonal close packing vaccant space are between three touching spheres whose centes lie at the coeners of an equilateral traingle
Reason :In hexagonal close packing voids are called voids are called square voids
View SolutionIf in a closest packed arrangement r is the radius of the sphere respresenting the tetrahedral void and R is the radius of the spheres in closest packed arrangement then
View SolutionHow many tetrahedral and octahedral void spaces are there for each sphere in close packing?
View SolutionAssertion:A tetrahedral void is surrounded by four spheres and an octahedral void is surrounded by six spheres.
Reason:The number of tetrahedral voids is double the number of close packed spheres and number of octahedral voids is equal to number of close packed spheres.
View SolutionWhile placing the second layer over that first layer , if the sphere of the second layer is above the void of the first layer, the void formed is
View SolutionHow many tetrahedral voids and octahedral voids are possible if the number of close packed spheres in two layers is N.
View SolutionExplain AAAA and ABABA and ABCABC type of three dimensional packing with the help of neat diagram. Voids : The empty spaces between the three dimensional layers are known as voids. There are two types of common voids possible. They are tetrahedral and octahedral voids. Tetrahedral void: A void formed by three spheres of a layer in contact with each other and also with a sphere on the top or bottom layer is a hole between four spheres. The spheres are arranged at the vertices of a regular tetrahedron such a hole or void is called tetrahedral void. Octahedral void: A hole or void formed by three spheres of a hexagonal layer and another three spheres of the adjacent layer is a hole between six spheres. The spheres are arranged at the vertices of a regular octahedron. Such a hole or void is called octahedral void.
View SolutionAssertion (A) : Packing efficiency of hcp and ccp structures is 74%.
Reason (R) : If the number of close packed spheres is N, then number of tetrahedral voids is N.
View Solution(A): ABAB ..... pattern of close packing gives hcp arrangement
(R): In hcp arrangement each sphere is associated with two tetrahedral voids
View Solution(A) In close packing of spheres a tetrahedral void is surrounded by four spheres whereas an octahedral void is surrounded by six spheres. (R) A tetrahedral void has a tetrahedral shape whereas an octahedral void has an octa-hedral shape.
View Solution(A): A void surrounded by a triangle of spheres capped by another sphere is called tetrahedral void.
(R) : Tetrahedral voids are in tetrahedral arrangement
View Solution
