Free energy, G=H-TS, is a state function that includes whether a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's energy that is disordered already, then (H-TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, ΔG=ΔH−TΔS
To see what this equation for free energy change has to do with spontaneity let us return to relationship.
ΔStotal=ΔSsys+ΔSsurr=ΔS+ΔSsurr
(It is generally understood that symbols without subscript refer to the system not the surroundings.)
ΔSsurr=−ΔHT, where ΔH is the heat gained by then system at constant pressure.
ΔStotal=ΔS−ΔHT
⇒TΔHtotal=ΔH−TΔS
⇒−TΔStotal=ΔH−TΔS
i.e. ΔG=−TΔStotal
From second law of thermodynamics, a reaction is spontaneous if ΔStotal is positive, non-spontanous if ΔStotal is negative and at equilibrium if ΔStotal is zero.
Since, −TΔS=ΔG and since ΔG and ΔS have opposite signs, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out at constant temperature and pressure.
If ΔG<0, the reaction is spontaneous.
If ΔG>0, the reaction is non-spontanous.
If ΔG=0, the reaction is at equilibrium.
In the equation, ΔG=ΔH−TΔS, temperature is a weighting factor that determine the relative importance of enthalpy contribution to ΔG.
Read the above paragraph carefully and answer the following questions based on above comprehension:
If an endothermic reaction is non-spontaneous at freezing point of water and becomes feasible at its boiling point, then
ΔG is -ve and ΔS is +ve
ΔH and ΔS both are +ve
ΔH and ΔS both are −ve
ΔH is positive and ΔS is negative.
The correct Answer is:B
To solve the question regarding the spontaneity of an endothermic reaction at different temperatures, we will analyze the relationship between ΔG (Gibbs free energy), ΔH (enthalpy change), and ΔS (entropy change) using the provided equations and concepts.
1. Understanding the Reaction:
- The reaction in question is endothermic, which means it absorbs heat. Therefore, ΔH > 0 (positive).
2. Spontaneity at Different Temperatures:
- At the freezing point of water (0°C or 273 K), the reaction is non-spontaneous. This implies that ΔG > 0.
- At the boiling point of water (100°C or 373 K), the reaction becomes feasible (spontaneous), which means ΔG < 0.
3. Using the Gibbs Free Energy Equation:
- The Gibbs free energy equation is given by:
ΔG=ΔH−TΔS
- Since ΔH is positive (endothermic), we can rewrite the equation as:
ΔG=positive value−TΔS
4. Analyzing at Freezing Point (0°C):
- At 273 K, since ΔG > 0 (non-spontaneous), we can deduce:
ΔH−(273K)ΔS>0
- Rearranging gives:
ΔH>(273K)ΔS
- This indicates that the positive enthalpy change is greater than the product of temperature and entropy change, leading to a positive ΔG.
5. Analyzing at Boiling Point (100°C):
- At 373 K, the reaction becomes spontaneous, so ΔG < 0:
ΔH−(373K)ΔS<0
- Rearranging gives:
ΔH<(373K)ΔS
- This suggests that at this higher temperature, the entropy change must be sufficiently large (positive) to outweigh the positive enthalpy change, resulting in a negative ΔG.
6. Conclusion on ΔS:
- Since ΔH is positive and the reaction is non-spontaneous at lower temperatures but becomes spontaneous at higher temperatures, we conclude that ΔS must be positive. This is because a positive ΔS contributes to making ΔG negative at higher temperatures.
Final Answer:
- ΔH is positive (since the reaction is endothermic).
- ΔS is positive (since the reaction becomes spontaneous at higher temperatures).
- The reaction in question is endothermic, which means it absorbs heat. Therefore, ΔH > 0 (positive).
- At the freezing point of water (0°C or 273 K), the reaction is non-spontaneous. This implies that ΔG > 0.
- At the boiling point of water (100°C or 373 K), the reaction becomes feasible (spontaneous), which means ΔG < 0.
- The Gibbs free energy equation is given by:
ΔG=ΔH−TΔS
- Since ΔH is positive (endothermic), we can rewrite the equation as:
ΔG=positive value−TΔS
- At 273 K, since ΔG > 0 (non-spontaneous), we can deduce:
ΔH−(273K)ΔS>0
- Rearranging gives:
ΔH>(273K)ΔS
- This indicates that the positive enthalpy change is greater than the product of temperature and entropy change, leading to a positive ΔG.
- At 373 K, the reaction becomes spontaneous, so ΔG < 0:
ΔH−(373K)ΔS<0
- Rearranging gives:
ΔH<(373K)ΔS
- This suggests that at this higher temperature, the entropy change must be sufficiently large (positive) to outweigh the positive enthalpy change, resulting in a negative ΔG.
- Since ΔH is positive and the reaction is non-spontaneous at lower temperatures but becomes spontaneous at higher temperatures, we conclude that ΔS must be positive. This is because a positive ΔS contributes to making ΔG negative at higher temperatures.
- ΔH is positive (since the reaction is endothermic).
- ΔS is positive (since the reaction becomes spontaneous at higher temperatures).
Topper's Solved these Questions
- THERMODYNAMICS AND THERMOCHEMISTRY Book:FIITJEEChapter:THERMODYNAMICS AND THERMOCHEMISTRY Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) COMPREHENSION -III
Explore 6 Videos
- THERMODYNAMICS AND THERMOCHEMISTRY Book:FIITJEEChapter:THERMODYNAMICS AND THERMOCHEMISTRY Exercise:MATRIX-MATCH TYPE
Explore 6 Videos
- THERMODYNAMICS AND THERMOCHEMISTRY Book:FIITJEEChapter:THERMODYNAMICS AND THERMOCHEMISTRY Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) COMPREHENSION -I
Explore 4 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:CHEMISTRY
Explore 747 Videos
- TRANSITION ELEMENTS & COORDINATION COMPOUNDSBook:FIITJEEChapter:TRANSITION ELEMENTS & COORDINATION COMPOUNDSExercise:MATCHIG LIST TYPE QUESTIONS
Explore 1 Video
Similar Questions
The second law of thermodynamics is a fundamental law of science. In this problem, we consider the thermodynamics of an ideal gas, phase transition, and chemical equilibrium.
Three moles of CO2 gas expands isothermally (in thermal contact with the surroundings, temperature =15.0∘C) against a fixed external pressure of 1.00¯. The initial and final volumes of the gas are 10.0L and 30.0L, respectively.
Select the correct order of the entropy change.
View SolutionMatch Column-I with Column-II
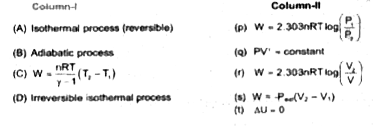
View SolutionThe state of a mole of an ideal gas changed from state A at pressure 2P and volume V follows four different processes and finally returns to initial state A reversibly as shown below in the graph. By intercepting the graph answer the following questions:
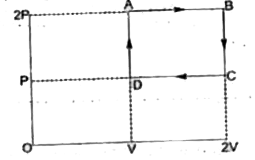
Which is the kind of process followed from state A to state B?
View SolutionFor a 3s-orbital
Φ(3s)=1a√3(1a0)3/2(6−6σ+σ2)∈−σ/2
where σ=2rZ3aσ
What is the maximum radial distance of node from nucleus?
View Solution
View SolutionFree Energy Change And Spontaneity
View SolutionFree enegry , G = H - TS , is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's enegry that is disordered already, then (H -TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered. Also, DeltaG = DeltaH - T DeltaS From the second law of thermodynamics, a reaction is spontaneous if Delta_("total")S is positive, non-spontaneous if Delta_("total")S is negative, and at equilibrium if Delta_('total")S is zero. Since, -T DeltaS = DeltaG and since DeltaG and DeltaS have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure. IF DeltaG lt 0 , the reaction is spontaneous. If DeltaG gt 0 , the reaction is non-spontaneous. If DeltaG = 0 , the reaction is at equilibrium. Read the above paragraph carefully and answer the following questions based on the above comprehension. For the spontaneity of a reaction, which statement is true?
View SolutionFree enegry , G=H−TS, is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's enegry that is disordered already, then (H−TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, ΔG=ΔH−TΔS From the second law of thermodynamics, a reaction is spontaneous if ΔtotalS is positive, non-spontaneous if ΔtotalS is negative, and at equilibrium if Δ'→talS is zero.
Since, −TΔS=ΔG and since ΔG and ΔS have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure.
IF ΔG<0, the reaction is spontaneous.
If ΔG>0, the reaction is non-spontaneous.
If ΔG=0, the reaction is at equilibrium.
Read the above paragraph carefully and answer the following questions based on the above comprehension.
A particular reaction has a negative value for the free energy change. Then at ordinary temperature
View SolutionFree enegry , G=H−TS, is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's enegry that is disordered already, then (H−TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, ΔG=ΔH−TΔS From the second law of thermodynamics, a reaction is spontaneous if ΔtotalS is positive, non-spontaneous if ΔtotalS is negative, and at equilibrium if Δ'→talS is zero.
Since, −TΔS=ΔG and since ΔG and ΔS have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure.
IF ΔG<0, the reaction is spontaneous.
If ΔG>0, the reaction is non-spontaneous.
If ΔG=0, the reaction is at equilibrium.
Read the above paragraph carefully and answer the following questions based on the above comprehension.
Which of the following is true for the reaction?
H2O(l)⇔H2O(g)at100∘C and 1 atmosphere
View SolutionFree enegry , G = H - TS , is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's enegry that is disordered already, then (H -TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered. Also, DeltaG = DeltaH - T DeltaS From the second law of thermodynamics, a reaction is spontaneous if Delta_("total")S is positive, non-spontaneous if Delta_("total")S is negative, and at equilibrium if Delta_('total")S is zero. Since, -T DeltaS = DeltaG and since DeltaG and DeltaS have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure. IF DeltaG lt 0 , the reaction is spontaneous. If DeltaG gt 0 , the reaction is non-spontaneous. If DeltaG = 0 , the reaction is at equilibrium. Read the above paragraph carefully and answer the following questions based on the above comprehension. If an endothermic reaction is non-spontaneous at freezing point of water and becomes feasible at its boiling point, then
View SolutionFree enegry , G = H - TS , is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's enegry that is disordered already, then (H -TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered. Also, DeltaG = DeltaH - T DeltaS From the second law of thermodynamics, a reaction is spontaneous if Delta_("total")S is positive, non-spontaneous if Delta_("total")S is negative, and at equilibrium if Delta_('total")S is zero. Since, -T DeltaS = DeltaG and since DeltaG and DeltaS have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure. IF DeltaG lt 0 , the reaction is spontaneous. If DeltaG gt 0 , the reaction is non-spontaneous. If DeltaG = 0 , the reaction is at equilibrium. Read the above paragraph carefully and answer the following questions based on the above comprehension. One mole of ice si converted to liquid at 273 K, H_(2)O(s) and H_(2)O(l) have entropies 38.20 and 60.03 J mol^(-1) dg^(-1) . Enthalpy change in the conversion will be
View SolutionFor a spontaneous chemical process, the free energy change is
View Solution(i) Spontaneity of a process can be determined from the entropy change and also from the Gibbs free energy change. But the Gibbs free energy change in more useful than entropy change to determine the spontaneity of a process. Explain it.
(ii) Show that Gibbs energy change of a system at certain temperature and pressure, ΔG=ΔH−TΔS.
View SolutionFree energy, G=H-TS, is a state function that includes whether a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's energy that is disordered already, then (H-TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, ΔG=ΔH−TΔS
To see what this equation for free energy change has to do with spontaneity let us return to relationship.
ΔStotal=ΔSsys+ΔSsurr=ΔS+ΔSsurr
(It is generally understood that symbols without subscript refer to the system not the surroundings.)
ΔSsurr=−ΔHT, where ΔH is the heat gained by then system at constant pressure.
ΔStotal=ΔS−ΔHT
⇒TΔHtotal=ΔH−TΔS
⇒−TΔStotal=ΔH−TΔS
i.e. ΔG=−TΔStotal
From second law of thermodynamics, a reaction is spontaneous if ΔStotal is positive, non-spontanous if ΔStotal is negative and at equilibrium if ΔStotal is zero.
Since, −TΔS=ΔG and since ΔG and ΔS have opposite signs, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out at constant temperature and pressure.
If ΔG<0, the reaction is spontaneous.
If ΔG>0, the reaction is non-spontanous.
If ΔG=0, the reaction is at equilibrium.
In the equation, ΔG=ΔH−TΔS, temperature is a weighting factor that determine the relative importance of enthalpy contribution to ΔG.
Read the above paragraph carefully and answer the following questions based on above comprehension:
A particular reaction has a negative value for the free energy change. Then at ordinary temperature.
View SolutionFor spontaneous reaction ,the change in free energy should be…
View SolutionI. Read the following passage and answer questions 1-5 that follows: Spontaneity means the feasibility of a reaction.Gibbs free energy (G) is the thermodynamic quantity which helps in predicting the spontaneity of a process G = H - TS The change in free energy is represented by Gibbs Helmoltz equation, DeltaH - DeltaH - TDeltaS For spontaneity of a process, DeltaG must be negative.It depends upon energy factor (DeltaH) and entropy factor (TDeltaS) . 1. What are the signs of DeltaH and DeltaS for the reactions : 2CI(g) to CI_(2)(g) ?
View Solution
