A motor cyclist is moving along the line x–y=2 and another motor cyclist is moving along the line x–y=4 find out their moving direction.
The correct Answer is:move parallel
To solve the problem of determining the moving direction of two motorcyclists moving along the lines x−y=2 and x−y=4, we can follow these steps:
Step 1: Understand the equations of the lines
The equations given are:
1. x−y=2
2. x−y=4
These equations represent straight lines in a two-dimensional coordinate system.
Step 2: Rearrange the equations
We can rearrange both equations into the slope-intercept form y=mx+b to identify their slopes.
For the first equation:
x−y=2⟹y=x−2
The slope m1=1.
For the second equation:
x−y=4⟹y=x−4
The slope m2=1.
Step 3: Analyze the slopes
Both lines have the same slope m1=m2=1. This indicates that the lines are parallel.
Step 4: Determine the direction of movement
Since the lines are parallel and have the same slope, the motorcyclists are moving in the same direction.
Conclusion
The two motorcyclists are moving in the same direction along their respective paths defined by the lines x−y=2 and x−y=4.
---
The equations given are:
1. x−y=2
2. x−y=4
We can rearrange both equations into the slope-intercept form y=mx+b to identify their slopes.
x−y=2⟹y=x−2
The slope m1=1.
x−y=4⟹y=x−4
The slope m2=1.
Both lines have the same slope m1=m2=1. This indicates that the lines are parallel.
Since the lines are parallel and have the same slope, the motorcyclists are moving in the same direction.
The two motorcyclists are moving in the same direction along their respective paths defined by the lines x−y=2 and x−y=4.
Topper's Solved these Questions
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - SHORT ANSWER TYPE (I) QUESTIONS
10 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - SHORT ANSWERS TYPE (II) QUESTIONS
10 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - PRACTICS-TEST (SECTION-D)
1 Videos
- POLYNOMIALSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - POLYNOMIALSEXERCISE - Practice test
10 Videos
Similar Questions
A ray moving along the line px+qy=1, after striking a mirror placed along the line y=3, is reflected along the line
View SolutionTwo particles start from the point (2,−1), one moving 2 units along the line x+y=1 and the other 5 units along the line x−2y=4. If the particles move towards increasing y, then their new positions are
View Solution
Knowledge Check
A particle is moving along a straight line.
AIf the acceleration of the particle is more than that of another object, the particle is moving faster.BIf the acceleration is positive, the speed must be increasing.CIf the acceleration and the velocity have the same sign, the speed must be increasing.DIf the acceleration is zero, the velocity is constant but the speed may be changing.A ray travelling along the line 3x - 4y = 5 after being reflected from a line l travels along the line 5x + 12y = 13. Then, the equation of the line l is
Ax+8y= 0Bx=8yCX + 4y = 65D32x - 4y = -65The drawing shows velocity (v) versus time (t) graphs for two cyclists moving along the same straight segment of a highway from the same point. The second cyclist starts moving at t=3min. At what time do the two cysclist meet ?
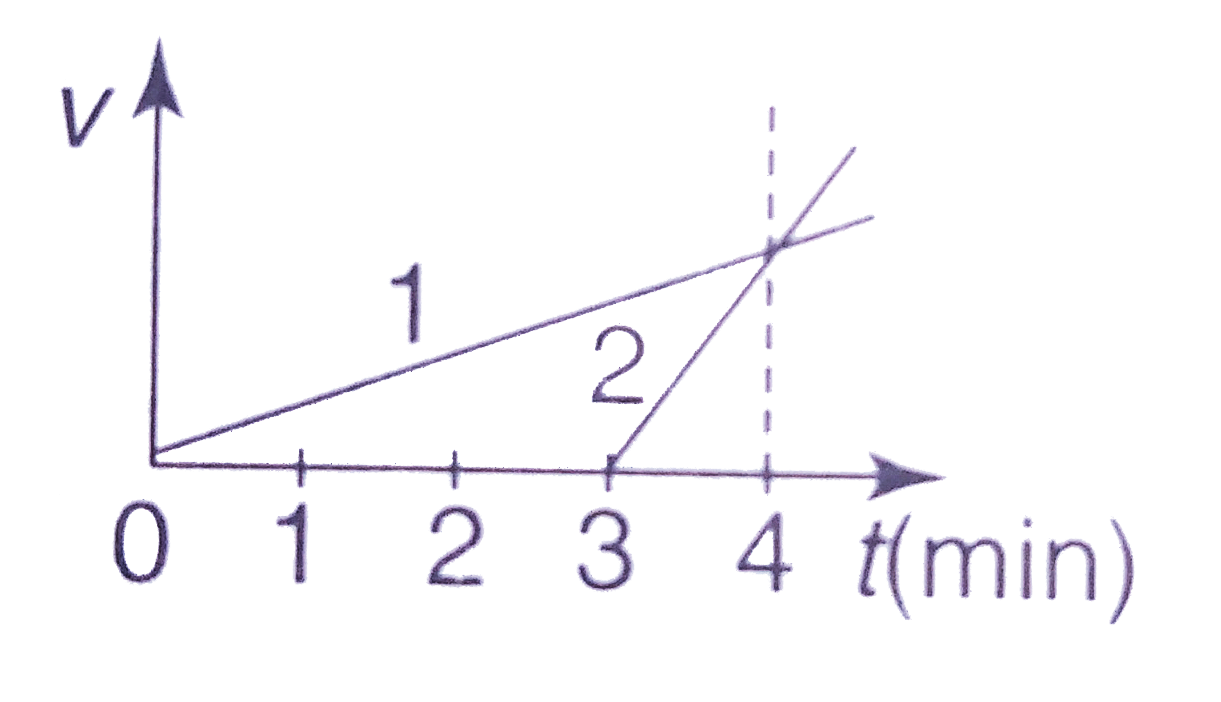 A4 minB6 minC8 minD12 min
A4 minB6 minC8 minD12 min
Why does a motorcyclist moving along a level curve at high speed have more than a cyclist moving along the same curve at low speed?
View SolutionTwo particles start from point (2, -1), one moving two units along the line x+ y = 1 and the other 5 units along the line x - 2y = 4, If the particle move towards increasing y, then their new positions are:
View SolutionFind the reflection of a point (2,3) along the line y=−x
View SolutionThe incident ray is along the line 3x−4y−3=0 and the reflected ray is along the line 24x+7y+5=0. Find the equation of mirrors.
View SolutionIf a force is applied at an angle to a body moving along a straight line:
View Solution
