Rate law for the elementary reaction 2AB→k1A2+B2 will be:
Rate =−d[AB]dt=k1[AB]2
Rate =−d[A2]dt=k1[AB]2
Rate =d[B2]dt=k1[AB]2
Rate =−d[A2]dt=k1[AB]22
The correct Answer is:C
To determine the rate law for the elementary reaction 2ABk1−→A2+B2, we will follow these steps:
1. Identify the Reaction:
The given reaction is 2ABk1−→A2+B2. Here, AB is the reactant, and A2 and B2 are the products.
2. Understand Elementary Reactions:
An elementary reaction is a single-step reaction where the reactants convert directly to products in one step. The rate law for such reactions can be derived directly from the stoichiometry of the reaction.
3. Write the Rate Law:
For an elementary reaction, the rate law can be expressed in terms of the concentrations of the reactants raised to the power of their stoichiometric coefficients.
- In this case, the stoichiometric coefficient of AB is 2.
- Therefore, the rate law can be written as:
Rate=k1(AB)2
4. Determine the Overall Order of the Reaction:
The overall order of the reaction is the sum of the powers of the concentration terms in the rate law. Since we have (AB)2:
- The overall order = 2.
5. Final Expression:
Thus, the rate law for the reaction 2ABk1−→A2+B2 is:
Rate=k1(AB)2
The given reaction is 2ABk1−→A2+B2. Here, AB is the reactant, and A2 and B2 are the products.
An elementary reaction is a single-step reaction where the reactants convert directly to products in one step. The rate law for such reactions can be derived directly from the stoichiometry of the reaction.
For an elementary reaction, the rate law can be expressed in terms of the concentrations of the reactants raised to the power of their stoichiometric coefficients.
- In this case, the stoichiometric coefficient of AB is 2.
- Therefore, the rate law can be written as:
Rate=k1(AB)2
The overall order of the reaction is the sum of the powers of the concentration terms in the rate law. Since we have (AB)2:
- The overall order = 2.
Thus, the rate law for the reaction 2ABk1−→A2+B2 is:
Rate=k1(AB)2
Similar Questions
For and elementary reaction
2Ak1⇐⇒k2B, the rate of disappearance of A iss equal to
(a) 2k1k2[A]2
(b) −2k1[A]2+2k2[B]
( c) 2k1[A]2−2k2[B]
(d) (2k1−k2)[A]View SolutionFor the elementary reaction 2A+B2→2AB. Calculate how much the rate of reaction will change if the volume of the vessel is reduced to one third of its original volume?
View Solution
Knowledge Check
- Question 1 - Select One
The differential rate law equation for the elementary reaction A+2Bk−−→3C, is
A−d[A]dt=d[B]dt=d[C]dt=k[A][B]2B−d[A]dt=12d[b]dt=13d[C]dt=k[A]2[B]C−d[A]dt=12d[b]dt=13d[C]dt=k[A][B]2DNone of these - Question 2 - Select One
Rate law for the reaction, A+2B→C is found to be
Rate =k[A][B]
Concentration of reactant 'B' is doubled keeping the concentration of 'A' constant, the value of rate constant will be _______Athe sameBdoubledCquadrupledDhalved - Question 3 - Select One
For a hypotherical elementary reaction
where k1k2=12
Initailly only 2 moles of A are present.
The sum of mole of (B) are ( C) is :A2B3C1D4
The standard Gibbs free energy change of for the reaction, 2AB⇔A2+B2 is 11.8 KJ at 230 K and 1 atm. Calculate degree of dissociation of AB at 230 K.
View SolutionFor a hypotherical elementary reaction
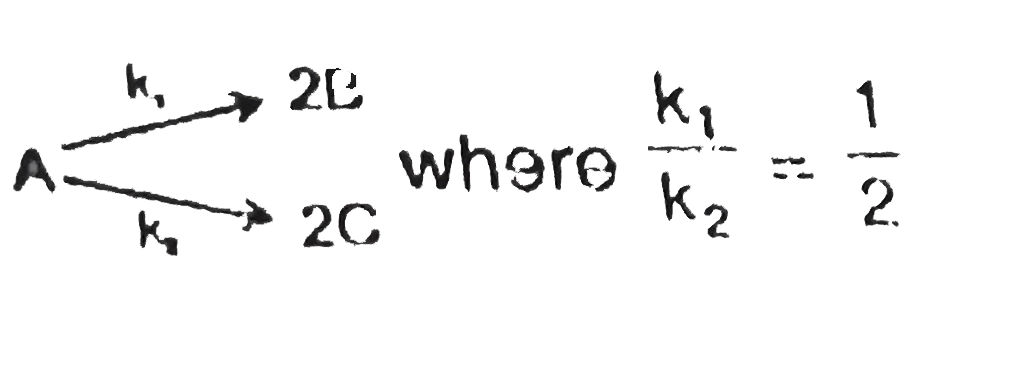where k1k2=12
Initailly only 2 moles of A are present.
Number of moles of B are:View SolutionFor a hypotherical elementary reaction
where k1k2=12
Initailly only 2 moles of A are present.
The total number of moles A,B and C at the end of 50% reaction are :View SolutionThe rate of the elementary reaction, A2(g)+B2(g)⇔2ABg is given by rate =1.7×10−18[A2][B2]. The rate of decomposition of gaseous AB to A2andB2 is given by rate =2.4×10−21[AB]2. The equilibrium constant, for the formation of AB from A2andB2 is
View SolutionA second order reaction between A and B is elementary reaction:
A+B → Product
rate law expression of this reaction will be:View Solution