Instantaneous angle (in radian) between string of a simple pendulum and verical is given by θ=π180sin2πt. Find the length of the pendulum if g=π2m/s2.
The correct Answer is:0.25m
Step by step video, text & image solution for Instantaneous angle (in radian) between string of a simple pendulum and verical is given by theta = (pi)/(180) sin2pit. Find the length of the pendulum if g = pi^(2) m//s^(2). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II37videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I26videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise24videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
Knowledge Check
- Question 1 - Select One
The period of a simple pendulum is double, when its length is increased by 1.2 m. The original length of the simple pendulum is
A0.2 mB0.3 mC0.4 mD0.5 m - Question 2 - Select One
A simple pendulum is oscillating at 34th of a second, where g = 980 cm sec2, the length of the pendulum is
A55.85 cmB48.5 cmC13.96 cmD42.2 cm - Question 3 - Select One
The instantaneous displacement of a simple pendulum oscillator is given by x=Acos(ωt+π4)Its speed will be maximum at time
Aπ4ωBπ2ωCπωD2πω
Find the length of seconds pendulum at a place where g=π2m/s2.
View SolutionIf sin(πcosθ)=cos(πsinθ) . Find sin(2θ)
View SolutionFigure shows the kinetic energy K of a simple pendulum versus its angle θ from the verticle. The pendulum bob has mass 0.2kg. If the length of the pendulum is equal to ng meter. Then find n(g=10m/s2)
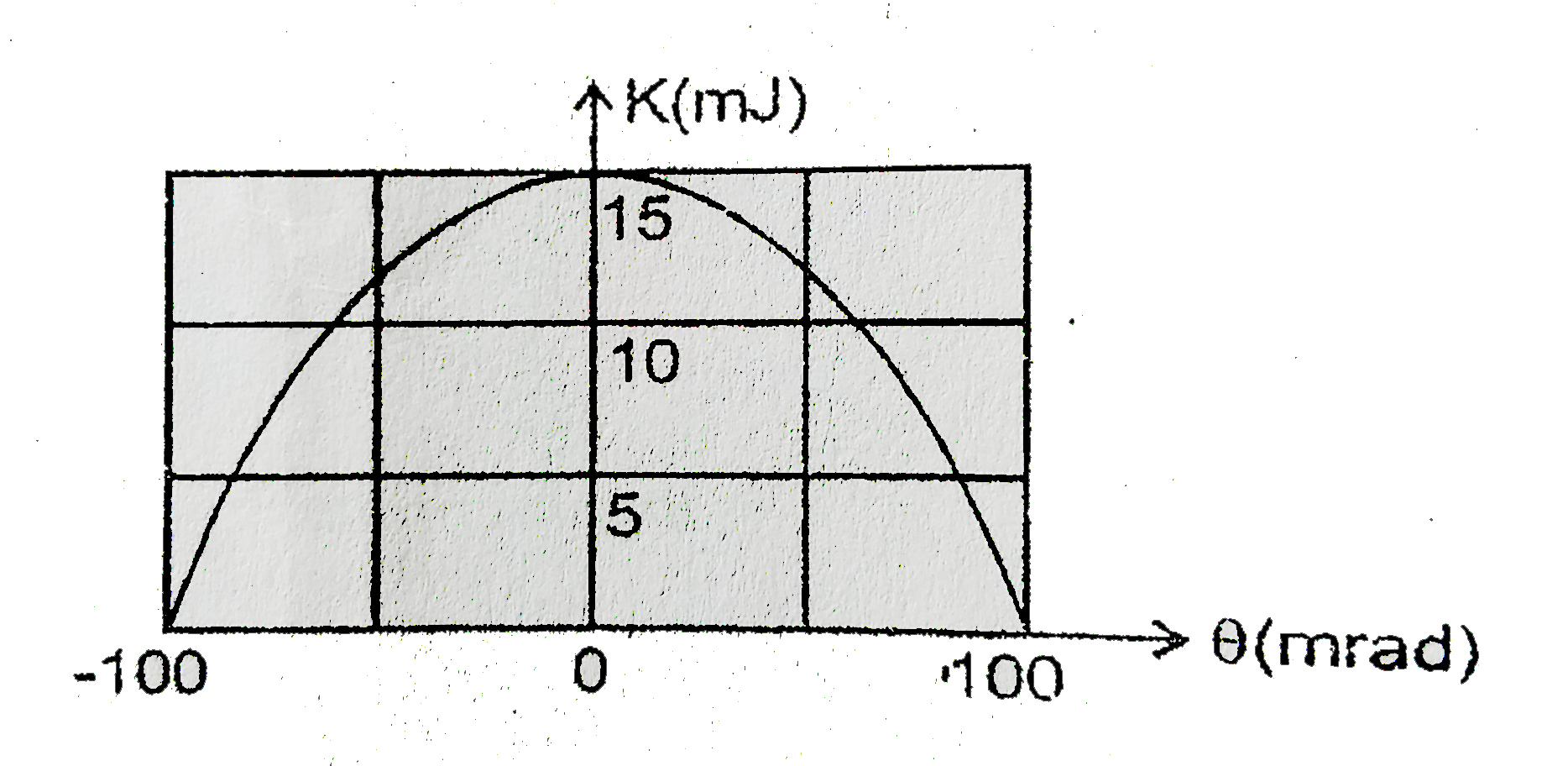 View Solution
View SolutionThe instantaneous displacement of a simple pendulum oscillator is given by x=Acos(ωt+π4)Its speed will be maximum at time
View SolutionA graph is drawn between the displacement and time taken for the oscillations of a simple pendulum. The length of the penddulum is _______ m ( if g = 10 s−2andπ2=10)
View Solution

