A toy car of mass m is having two similar rubber ribbons attached to it as shown in the figure. The force constant of each rubber ribbon is k and surface is frictionless. The car is displaced from mean position by xcm and released. At the mean position the ribbons are undeformed. Vibration period is

2π√m(2k)k2
12π√m(2k)k2
2π√mk2
2π√mk+k
The correct Answer is:C
Step by step video, text & image solution for A toy car of mass m is having two similar rubber ribbons attached to it as shown in the figure. The force constant of each rubber ribbon is k and surface is frictionless. The car is displaced from mean position by x cm and released. At the mean position the ribbons are undeformed. Vibration period is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I26videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II1videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I25videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
A trolley of mass 3.0 kg is connected to two identical rubber bands each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from an equilibrium position by 5.0 cm and released, what is the period of ensuing oscillations?
 View Solution
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
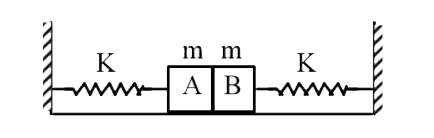 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
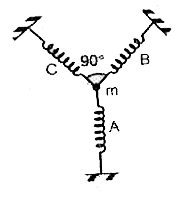 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1) - Question 2 - Select One
Two springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :
 AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k - Question 3 - Select One
A pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
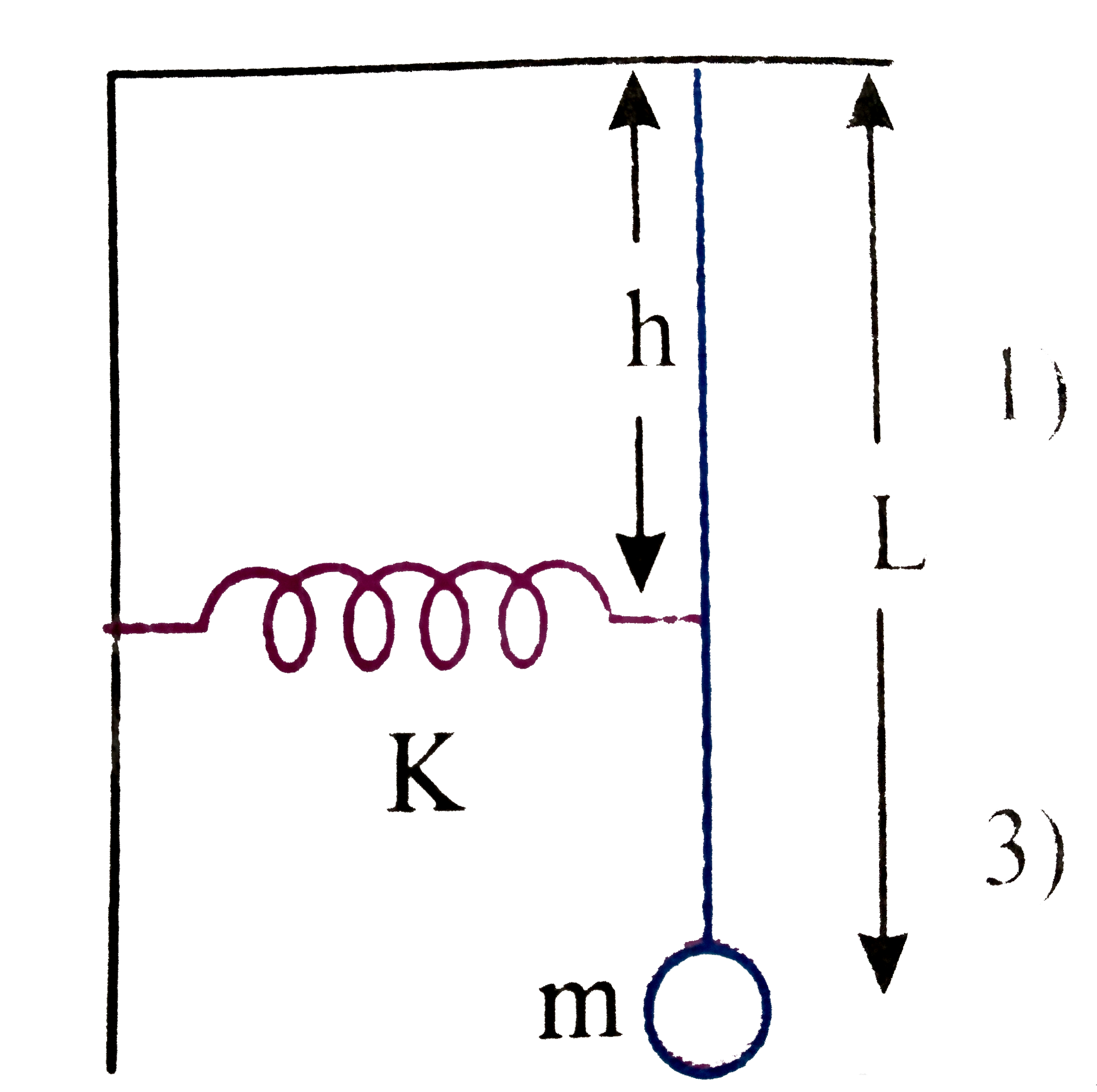 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 View Solution
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is
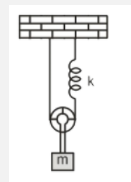 View Solution
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 View Solution
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beView SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 View Solution
View Solution

