Use the mirror equation to show that $(a)$ an object placed btween $f$ and $2 f$ a concave mirror produces a real image beyond $2 f (b)$ a convex mirror always produces a virtual image independent of the location of the objcet. $(c)$ an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.

Text Solution

Verified by Experts

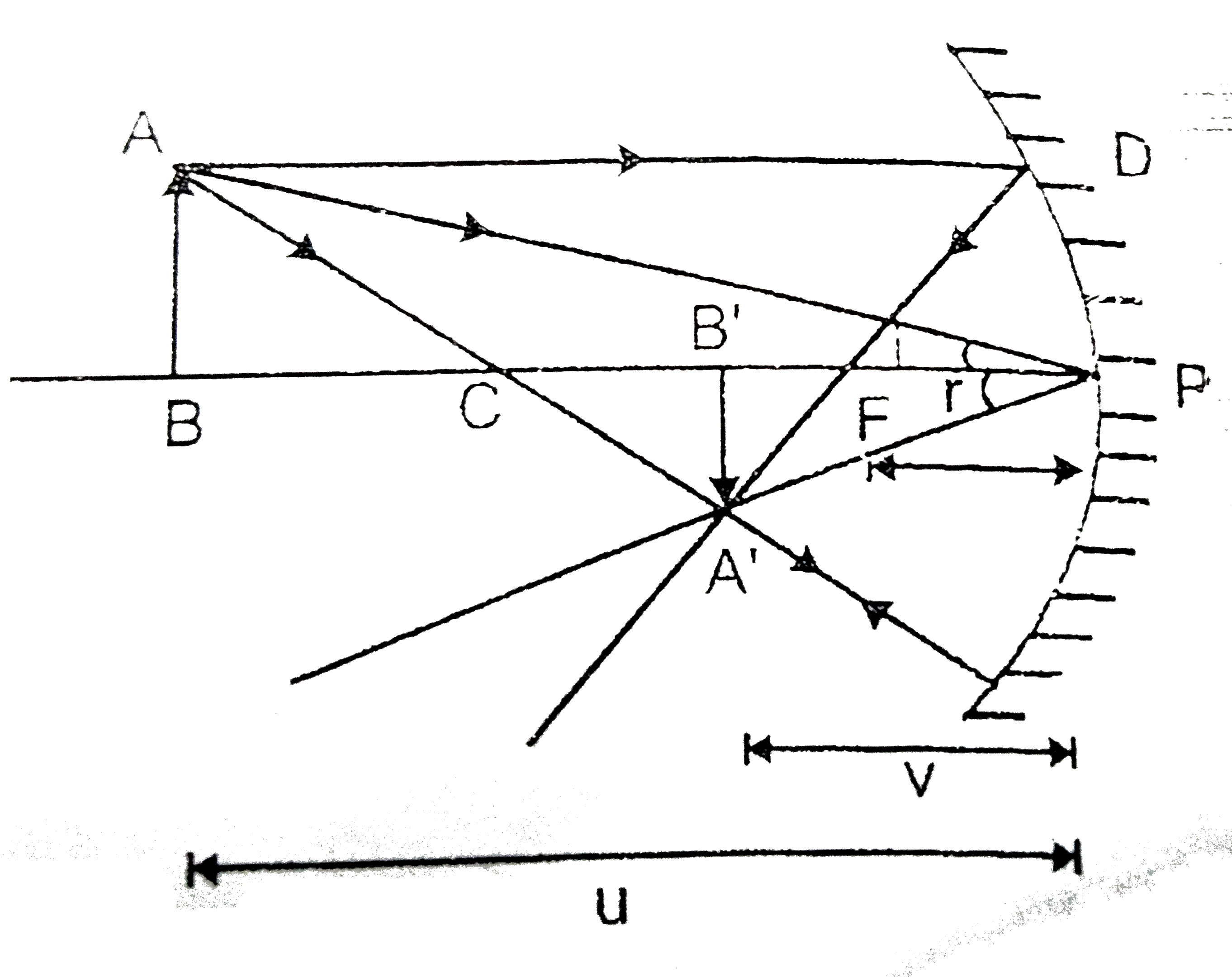
(a) As $Δ s A B C$ and $A' B' C$ are similar
$∴ \frac{A B}{A' B'} = \frac{C B}{C B'} \dots \dots . . (I)$
Again as $Δ s A B P$ and $A' B' P$ are similar
$\frac{A B}{A' B'} = \frac{P B}{C B'} \dots \dots . . (i i)$
From $(i)$ and $(i i)$
$\frac{A B}{A' B} = \frac{P B}{P B'} \dots \dots . (i i i)$
Measuring all distance from $P$ , we have
$C B = P B - P C$
$C B' = P C - P B'$
$∴$ from $(i i i)$
$\frac{P B - P C}{P C - P B'} = \frac{P B}{P B'} ... ... . . (i v)$
Using New Cartisian sign conventions,
$P B = - u$
$P C = - R$
$P B' = - v$
We get from $(i v)$
$\frac{- u + R}{- R + v} = \frac{- u}{- v}$
or $+ u R - u v = u v - v R$
$u R + v R = 2 u v$
Dividing both sides by $u v R$ , we get
$\frac{1}{v} + \frac{1}{u} = \frac{2}{R}$
As $\frac{1}{v} + \frac{1}{u} = \frac{2}{R} = \frac{2}{2 f} = \frac{1}{f}$
$\Rightarrow \frac{1}{v} + \frac{1}{u} = \frac{1}{f}$

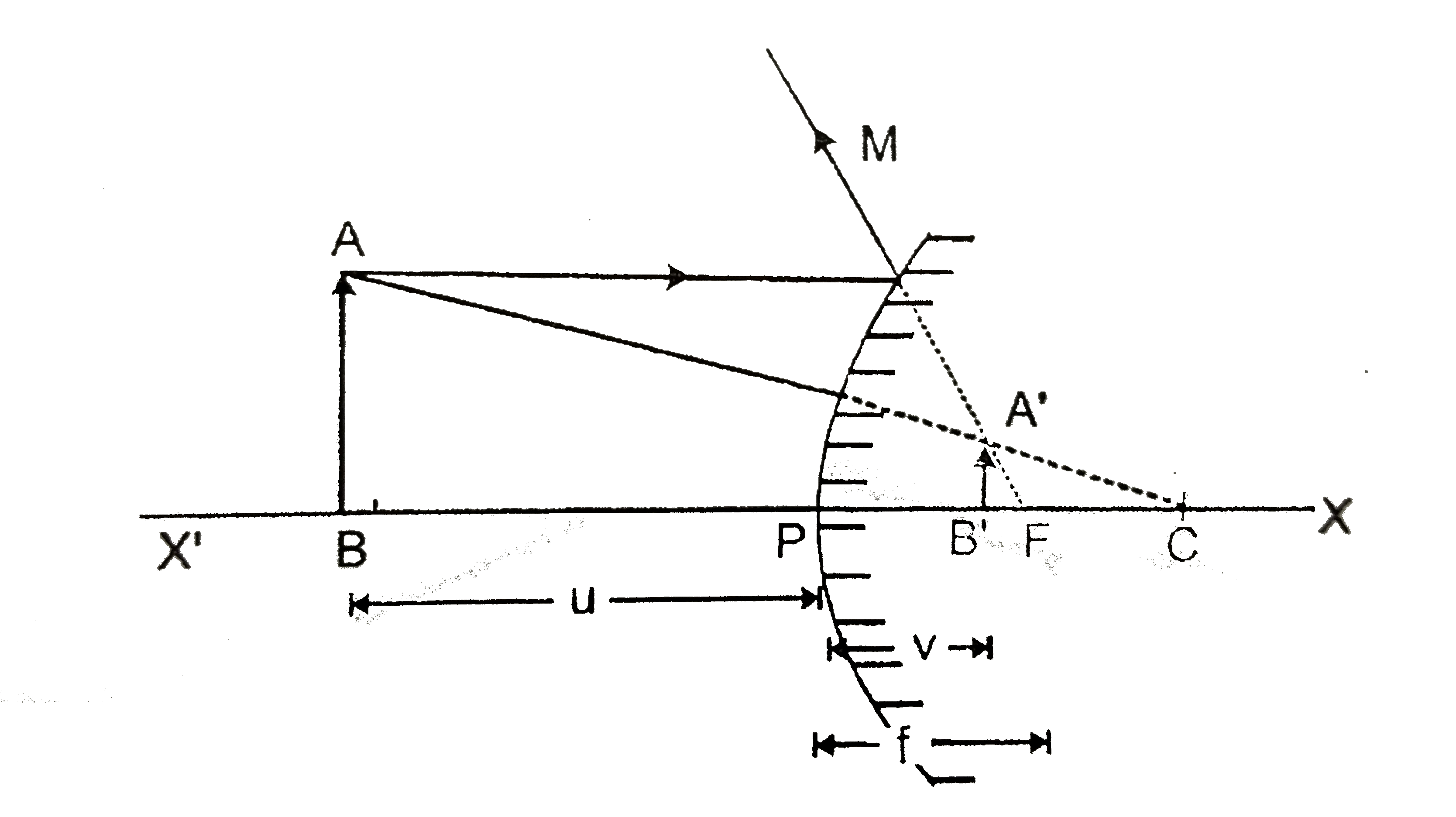
(b) According to sign conventions,
$P B' = - u, P B' = + v$
$P B = f, P C = 2 f$
$Δ s A B C$ and $A' B' C$ are similar
$∴ \frac{A B}{A' B'} = \frac{C B}{B' C}$
But all distances along the principal axis should be measured from the pole of the mirror.
$\frac{A B}{A' B'} = \frac{P C + P B}{P C - P B'}$
Since the aperture of the mirror is small therefore $M P$ can be regarded as a straight line.
$Δ s M P F$ and $A' B' F$ are similar
$\frac{M P}{A' B'} = \frac{P F}{B' F} = \frac{P F}{P F - P B'}$ or $\frac{A B}{A' B'} = \frac{f}{f - v} ... ... . . (i i)$
from $(i)$ and $(i i)$
$\frac{2 f - u}{2 f - v} = \frac{f}{f - v}$
$2 f^{2} - 2 f v - u f + u v = 2 f^{2} - v f$
$- f v - u f + u v = 0$
$u v = f v + f u$
Dividing by $u v f$ , we get
$\frac{1}{f} = \frac{1}{u} + \frac{1}{v}$

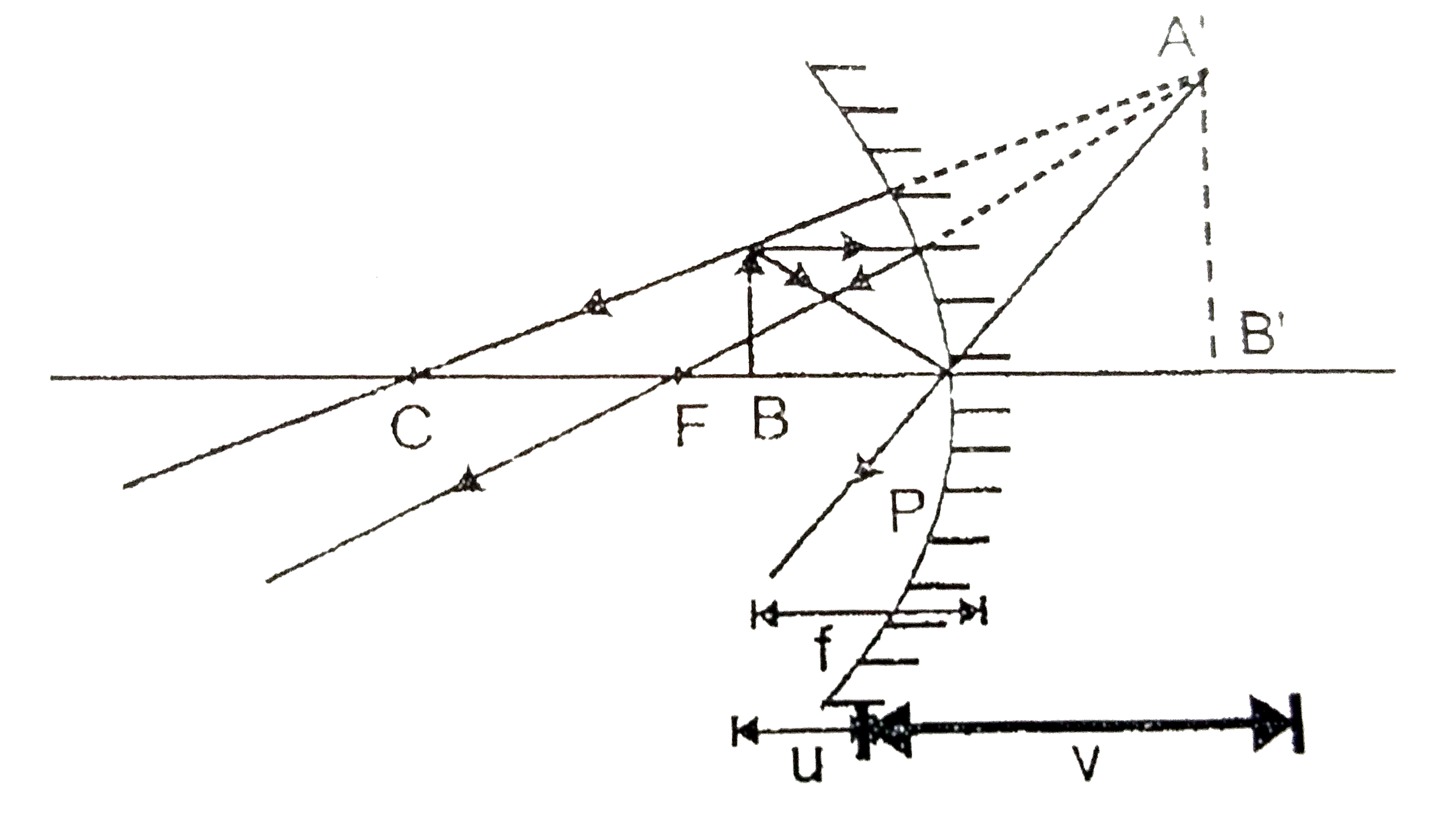
(c) $\frac{P B - P C}{P C - P B'} = \frac{P B}{P B'} ... ... . . (i)$
Proceeding as above, we get
$\frac{C B}{C B'} = \frac{P B}{P B'} ... ... ... . . (i i)$
Measuring all distance from $O$ , we get
$C B = P C - P B$
$C B' = P C + P B$
From $(i)$
$\frac{P C - P B}{P C + P B'} = \frac{P B}{P B'}$
Using New cartisian sign conventins,
PB=-u,PB=+v $< b r >$ PC=-R=(-R+u)/(-R+V)=(-u)/(v) $< b r > or$ uR-uv=vR+uv $< b r >$ uR+vR=2 uv $< b r > D i v g ⊥ h s s b y$ uvR $, w e \geq t < b r >$ (1)/(v)+(1)/(u)=(2)/(R)=(2)/(2f)=(1)/(f) , (1)/(v)+(1)/(u)=(1)/(f)

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A virtual object placed between the pole and principle focus of a convex mirror produce and image which is
Areal, magnified and erect.
Bvirtual, diminished and inverted.
Cvirtual, maginified and inverted.
Dreal, diminshed and invrted.

RESONANCE-GEOMATRICAL OPTICS -Exercise-3

Home
Ask Doubt
Profile