A particle of massM and positive charge Q, moving with a constant velocity →u1=4ˆims−1, enters a region of uniform static magnetic field , normal to the x−y plane. The region of the magnetic field extends from x=0 to x=L for all values of y. After passing through this region, the particle emerges on the other side after 10milliseconds with a velocity →u2=2(√3ˆi+ˆj)ms−1 . The correct statement(s) is (are)
The direction of the magnetic field is −z-direction.
The direction of the magnetic field is +z-direction.
The magnitude of the magnetic field 50πM3Q units.
The magnitude of the magnetic field 100πM3Q units.
The correct Answer is:A,C
Component of final velocity of particle is in positive y direction.
Centre of circle is present on positive y axis.so magnetic field is present in negative z-direction Angle of deviation is 30∘ because
tanθ=vyvx=1√3
θ=π6
ωt=θ
θ=QBMt
B=MθQt
B=(500Mπ3Q)
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-227videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-329videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION- 35videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
- BOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force . The path of the particle is a circle .
View SolutionA particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x = a to x = b. The minimum value of v required so that the particle can just enter the region x lt b is
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x=a to x=b. The minimum value of v required so that the particle can just enter the region x>b is
AqbBmBq(b−a)BmCqaBmDq(b+a)B2m - Question 2 - Select One
A particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circularBcircular, If v×B=0Ccircular,If v.B=0DNone of these - Question 3 - Select One
A particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x=a to x=b. The minimum value of v required so that the particle can just enter the region x>b is
Aqb B/mBq(b−a)B/mCqa B/mDq(b+a)B/2m
A particle of mass m and charge q moving with velocity v enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected?
View SolutionFour particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
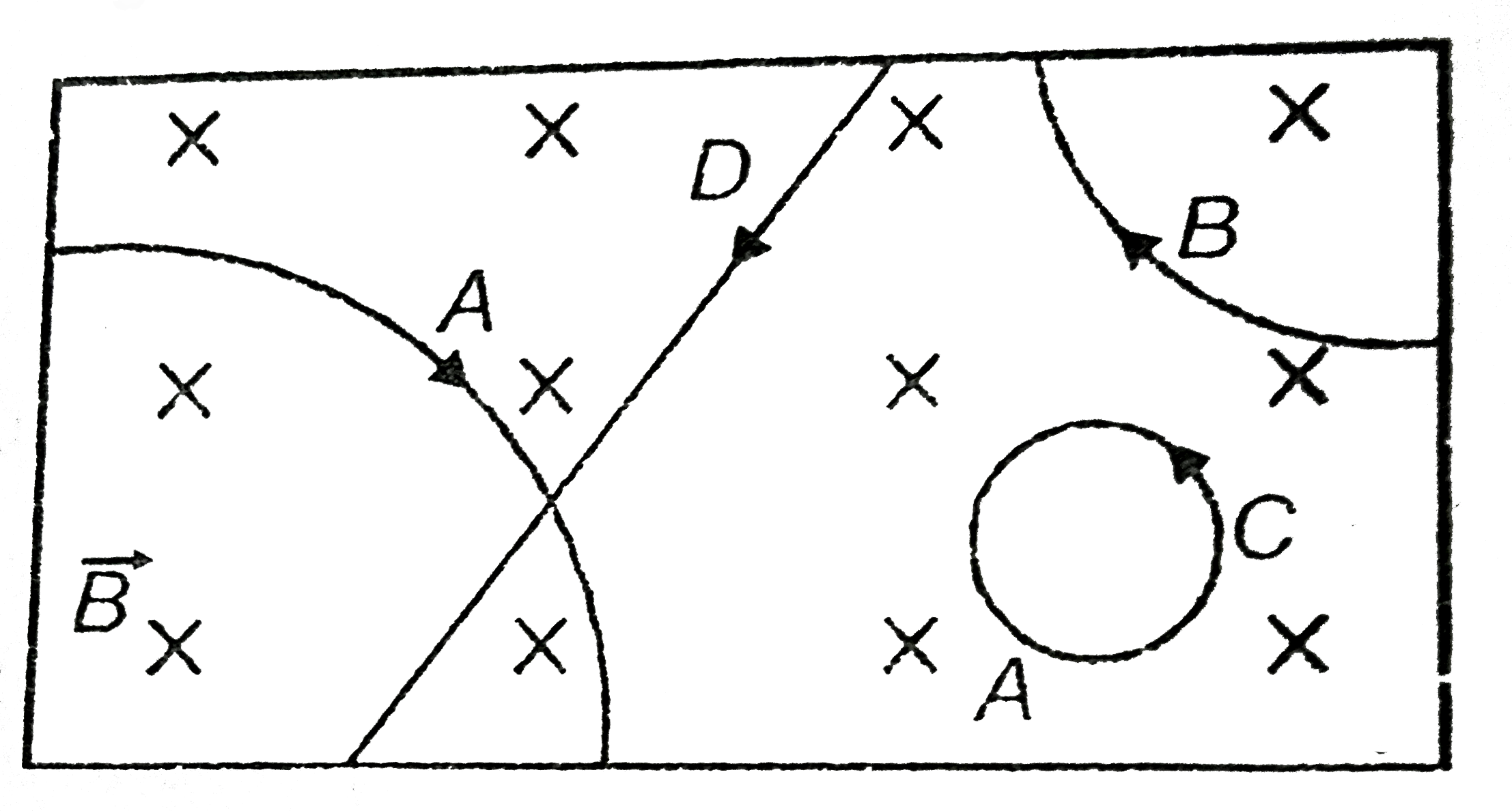 View Solution
View SolutionA charged particle moves through a region of uniform magnetic field perpendicularly. Is the momentum of particle affected ?
View SolutionA particle of the mass m and cgharge q moves with a constant velocity v along the positive x−direction.Itentersaregionconta∈∈gauniformmag≠ticfieldBdirectedalongtheminiμmvalueofvrequiredsotˆthepartic≤canjustentertheregion xgtb is
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View Solution

