परमाणु के प्रारंभिक प्रतिरूप में यह माना गया था कि आवेश Ze का बिंदु आमाप का घनात्मक नाभिक होता है जो त्रिज्या तक एकसमान घनत्व के ऋणावेश से घिरा हुआ है। परमाणु पूर्ण रूप में विधुत उदासीन है। इस प्रतिरूप के नाभिक से r दूरी पर विधुत क्षेत्र कितना है ?
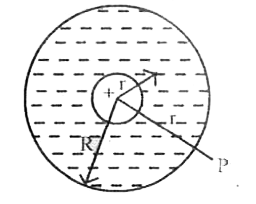
चूँकि परमाणु विधुत उदासीन होता है अतः यदि नाभिक में धनात्मक आवेश Ze विधमान है तो नाभिक के चारो ओर सममित रूप से वितरण ऋणात्मक आवेश का परिमाण भी Ze होगा।
ऋणात्मक आवेश के लिए आवेश घनत्व
ρ=Ze43πR3=3Ze4πr3 . . .(1)
(i) जब बिन्दु P परमाणु के बाहर स्थित है (r>) - इस स्थिति में परमाणु के चारो ओर r त्रिज्या के गोलीय गाउसियन पृष्ठ की गाउसियन पृष्ठ द्वारा परिबद्ध आवेश Σq=(+Ze)+(−Ze)
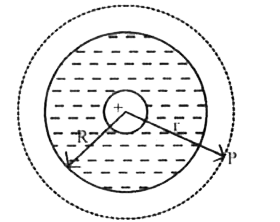
या Σq=0
अतः ϕ=∮→E.d→S=Σq∈0 से
Eout=0 (∵Σq=0)
(ii) जब बिन्दु P, परमाणु के अन्दर स्थित है (r<R) - इस स्थिति में गोलीय गाउसियन पृष्ठ द्वारा परिबद्ध कुल आवेश
Σq=(+Ze)+ (r त्रिज्या के गोले में ऋणात्मक आवेश)
Σq=(+Ze)+(−43πr3ρ)
Σq=(+Ze)−(43πr3×3Ze4πR3
Σq=Ze−Zer3R3
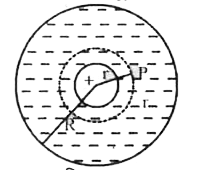
अतः गाउस से
ϕ=∮→E.d→S=Σq∈o=Ze∈0(1−r3R3) . . . (1)
चूँकि गोलीय गाउसीयन पृष्ठ पर सममिति के कारण सर्वत्र विधुत गए क्षेत्रफल अल्पांश के अनुदिश या विपरीत होगी
अतः समी (1) से
E∮dS=Ze∈0(R3−r3R3) ∵∮dS=4πr2
⇒ E×4πr2=Ze∈0(R3−r3R3)
या Ein=Ze4π∈0(1r2−rR3)
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - गाऊस का नियम एव इसके अनुप्रयोग EXERCISE - अतिलघुरात्मक प्रश्न28videos
गाऊस का नियम एव इसके अनुप्रयोग
- BOOK - SCIENCE PUBLICATIONCHAPTER - गाऊस का नियम एव इसके अनुप्रयोग EXERCISE - पाठ्यपुस्तक के प्रश्न - उत्तर (वस्तुनिष्ठ प्रश्न)11videos
गाऊस का नियम एव इसके अनुप्रयोग
- BOOK - SCIENCE PUBLICATIONCHAPTER - गाऊस का नियम एव इसके अनुप्रयोग EXERCISE - अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न)3videos
गाऊस का नियम एव इसके अनुप्रयोग
- BOOK - SCIENCE PUBLICATIONCHAPTER - किरण प्रकाशिकी EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)11videos
किरण प्रकाशिकी
- BOOK - SCIENCE PUBLICATIONCHAPTER - चुम्बकत्व एवं चुम्बकीय पदार्थो के गुणEXERCISE - अन्य महत्त्वपूर्ण प्रश्न ( आंकिक प्रश्न )23videos
चुम्बकत्व एवं चुम्बकीय पदार्थो के गुण
Similar Questions
सदिश क्षेत्रफल की सीधा निर्धारण किस प्रकार की जाती है ?
09:03View Solutionएक समरूप आवेशित ठोस अचालक गोले के कारण विधुत क्षेत्र की तीव्रता अधिकतम होती है।
04:43View Solutionमिमी त्रिज्या वाले एक लम्बे, सीधे तार पर विधुत आवेश समान रूप से वितरित है। तार की 1 सेमी लम्बाई पर आवेश का मान Q कूलॉम है। एक अन्य बेलनाकार पृष्ठ जिसकी त्रिज्या 50 सेमी तथा लम्बाई 1 मी है , इस तार को समान (सम्मिट) रूप से घेरे है , जिसकी चित में दर्शाया गया है। इस बेलनाकार पृष्ठ से गुजरने वाले कुल वैधुत अभिवाल (फ्लक्स) का मान ज्ञात कीजिए
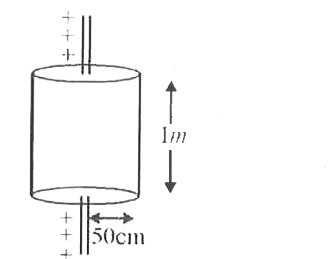 04:52View Solution
04:52View Solution2.5cm साइज की कोई छोटी मोमबत्ती 36 cm वक्रता त्रिज्या के किसी अवतल दर्पण से 27 cm दूरी पर रखी है। दर्पण से किसी परदे को कितनी दूरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिंब परदे पर बने। प्रतिबिंब की प्रकृति और साइज का वर्णन कीजिए। यदि मोमबत्ती को दर्पण की ओर ले जाएँ ,तो परदे को किस ओर हटाना पड़ेगा ?
07:33View Solutionएक परिनालिका में पास -पास लपेटे गए 800 फेरे है , तथा इसका अनुप्रस्थ काट का क्षेत्रफल 2.5×10−4m2 है और इसमें 3.0A धारा प्रवाहित हो रही है। समझाइए कि किस अर्थ में यह परिनालिका एक छड़ चुम्बक कि तरह व्यवहार करती है ? इसके साथ जुड़ा हुआ चुंबकीय आघूर्ण कितना है ?
45:46View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?01:19:07View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
एकसमान विद्युत क्षेत्र का 20 cm भुजा के किसी घन से (जो इस प्रकार अभिविन्यासित है की उसके फलक निर्देशांक तलों के समांतर है ) कितना नेट फ्लक्स गुजरेगा ?44:14View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
43:13View Solution1 से 11 तक के पूर्णांकों में से यादृच्छया दो पूर्णांकों को चुना गया है | दोनों पूर्णांकों के विषय होने कि प्रायिकता ज्ञात करो यदि यह ज्ञात है कि दोनों पूर्णांकों का योग सम है |
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solutionपरमाणु क्या है |परमाणु मॉडल के बारे में संक्षिप्त जानकारी |परमाणु में कोण कोण से मूलभूत कण पाए जाते है |कोष, उपकोष एवं कक्षक से परिचय |इलेक्ट्रान का कक्षाओं में वितरण कैसे करते है |इलेक्ट्रानइक विन्यास कैसे लिखते है ?|सारांश
View Solutionआवेश का वितरण कितने प्रकार का होता है #!#रेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता
View Solutionविधुत विभव क्या होता है #!#बिंदु आवेश के लिए विभव का सूत्र
View Solutionविरंजक चूर्ण में इसके एक घटक के रूप में एक ऑक्सोअम्ल का लवण होता है। इस अम्ल का एनहाइड्राइड है:
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionऐडिनिन न्यूक्लिक अम्ल के न्यूक्लियोटाइडों के निर्माण में शामिल दो प्यूरीन क्षारों में से एक है। ऐडिनिन का अणुसूत्र CxHxNx होता है, तो 'x' का मान है
View Solution

