Cramer-এর নিয়ম প্রয়োগে সমাধান করx+y+z=3,a2x+b2y+c2z=a2+b2+c2, a3x+b3y+c3z=a3+b3+c3 [a≠b≠cএবং ab+bc+ca≠0]
Step by step video & image solution for Cramer-এর নিয়ম প্রয়োগে সমাধান কর x+y+z = 3, a^2 x+ b^2 y+ c^2 z = a^2 + b^2 + c^2, a^3 x+ b^3 y+ c^3 z = a^3 + b^3 + c^3 [a ne b ne c এবং ab + bc + ca ne 0] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
সঠিক উত্তরটি নির্বাচন করো
∣∣ ∣∣abaabbabc∣∣ ∣∣ -এর মান হবে-
View Solutionদ্বিপদ বিভাজনের প্যারামিটার হল-
View Solution∫10cosnxdx
View SolutionIf (x)/(a)=(y)/(b)=(z)/(c), then show that (x^(3)+a^(3))/(x^(2)+a^(2))+(y^(3)+b^(3))/(y^(2)+b^(2))+(z^(3)+c^(3))/(z^(2)+c^(2))=((x+y+z)^(3)+(a+b+c)^(2))/((x+b+z)^(2)+(a+b+c)^(2))
View SolutionIf x:a=y:b=z:c, then prove that
x3a2+y3b2+z3c2=(x+y+z)3(a+b+c)2
View SolutionSuppose a, b and c are distinct and x,y and z are connected by the system of eqations x+ay+a2z=a3,x+by+b2z=b3andx+cy+c2z=c3.
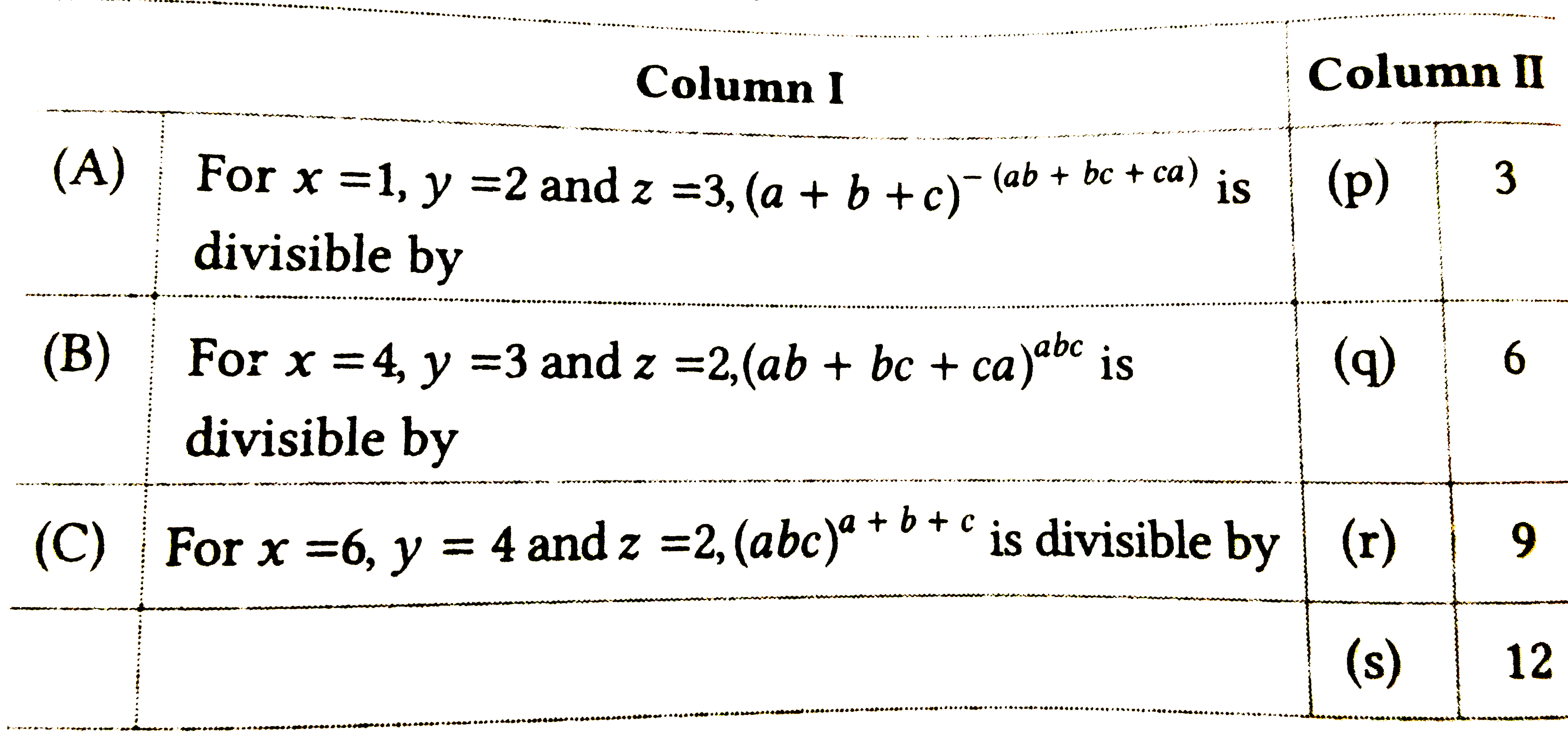
View Solutionसरणिक के गुण के आधार पर सिद्ध करें कि
(i) ∣∣ ∣ ∣∣xax+ayby+bzcz+c∣∣ ∣ ∣∣=0
(ii) ∣∣ ∣ ∣∣0ab2ac2a2b0bc2a2ccb20∣∣ ∣ ∣∣=2a3b3c3
View Solutionx+y+z=3,<br>a2x+b2y+c2z=a2+b2+c2,<br>a3x+b3y+c3z=a3+b3+c3
[a,b,c are unequal and ab+bc+ca ≠=0].
View Solutionयदि a3+b3+c3−Z=(a+b+c)(a2+b2+c2−ab−bc−ca) तो Z का मान बताइये।
View SolutionIf a,b,c,x,y and z be real numbers and x2+y2+z2=16;a2+b2+c2=9;ax+by+cz=12; the value of (a3+b3+c3)13(x3+y3+z3)13 is
View SolutionIf a, b, c, x, y and z be real numbers and x2+y2+z2=16 a2+b2+c2=9 ax+by+cz=12; the value of [a3+b3+c3]13[x3+y3+z3]13 is
View SolutionIf a, b, c, x, y and z be real numbers and x2+y2+z2=16, a2+b2+c2=9 and ax+by+cz=12; the value of (a3+b3+c3)13(x3+y3+z3)13 is
View SolutionThe solution of the system of equations a2x+ay+z=−a3,b2x+by+z=−b3,c2x+cy+z=−c3 is
(A) x=−(a+b+c),y=ab+bc+ca,z=−abc
(B) x=(a+b+c),y=ab+bc+ca,z=−abc
(C) x=−(a−b−c),y=ab+bc+ca,z=−abc
(D) None of these
View Solutionx : a = y : b = z : c হলে, প্রমাণ করি যে, x3a2+y3b2+z3c2=(x+y+z)3(a+b+c)2
View SolutionIf x sin a + y sin 2 a + z sin 3 a = sin 4 a x sin b + y sin 2 b + z sin 3 b = sin 4 b x sin c + y sin 2 c + z sin 3 c = sin 4 c the equation t^3 -(z/2)t^2 -((y+2)/4)t+((z-x)/8)=0,a,b,c,ne npi Is the origin of
View Solution
