lx+my=n সরলরেখা x2a2+y2b2=1 উপবৃত্তটির স্পর্শক হওয়ার শর্ত নির্ণয় করো।
Step by step video & image solution for lx+my=n সরলরেখা (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 উপবৃত্তটির স্পর্শক হওয়ার শর্ত নির্ণয় করো। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
সঠিক উত্তরটি নির্বাচন করো
y=f(x)সম্ভত লঞ্জের ওপর(x1,y1) বিন্দুতে অঙ্কিত অভিলম্বের নতি m হলে m =
View Solutionসঠিক উত্তরটি নির্বাচন করো
limx→0e3x−12x -এর মান হবে -
View SolutionThe line lx+my+n=0 will be a normal to the hyperbola b^(2)x^(2)-a^(2)y^(2)=a^(2)b^(2) if
View SolutionThe line lx+my=n is a normal to the ellipse x2a2+y2b2=1 , if
View SolutionIf the line lx+my+n=0 touches the hyperbola x2a2−y2b2=1. Then
View SolutionThe pole of the line lx+my+n=0 with respect to the hyperbola x2a2−y2b2=1, is
View SolutionThe line lx+my+n=0 is a normal to x2a2+y2b2=1, provided
View Solutionसिद्ध कीजिए कि रेखा lx+my+n=0 दीर्घवृत्त x2a2+y2b2=1 का अभिलम्ब है यदि a2l2+b2m2=(a2−b2)2n
View SolutionIf the line lx+my +n=0 touches the ellipse x2a2+y2b2=1 then
View SolutionThe condition that the line lx+my+n=0 to be a normal to the ellipse x2a2+y2b2=1 is
View SolutionIf lx+ my = 1 is a normal to the hyperbola x2a2−y2b2=1,thena2m2−b2l2=
View Solutionरेखा lx+my−n=0 दीर्घवृत्त x2a2+y2b2=1 को स्पर्श करेगी, यदि
View SolutionThe line lx+my=n is a normal to the ellipse x2a2+y2b2=1
View SolutionIf the line lx+my+n=0 touches the hyperbola x2a2−y2b2=1. Then
View SolutionThe pole of the line lx+my+n=0 with respect to the hyperbola x2a2−y2b2=1, is
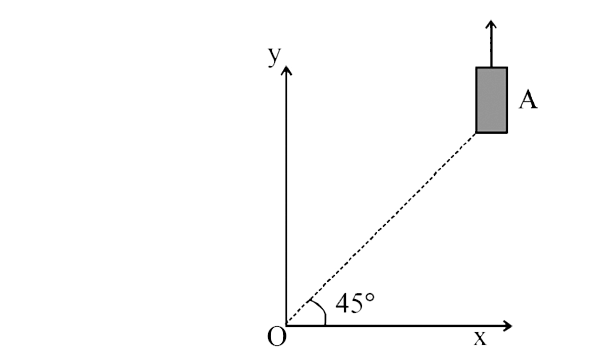
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
View Solution
