কলনবিদ্যার সাহায্যে x2+y2=16 বৃত্তের যে স্পর্শকের প্রব্নতা (−43) তার সমীকরণ নির্ণয় করো।
Step by step video & image solution for কলনবিদ্যার সাহায্যে x^2+y^2=16 বৃত্তের যে স্পর্শকের প্রব্নতা (-frac(4)(3)) তার সমীকরণ নির্ণয় করো। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
সঠিক উত্তরটি নির্বাচন করো
y=f(x)সম্ভত লঞ্জের ওপর(x1,y1) বিন্দুতে অঙ্কিত অভিলম্বের নতি m হলে m =
View Solutionসঠিক উত্তরটি নির্বাচন করো
limx→0e3x−12x -এর মান হবে -
View Solution9x2+25y2=225 উপবৃত্ত দুটির নাভিলম্বের দৈর্ঘ্য নির্ণয় করো।
View Solution6 সেমি ব্যাসার্ধবিশিষ্ট বৃত্তে কোনো চাপ 20∘17′সম্মুখ।কোণউৎপন্নকরে।৪ সেমি ব্যাসার্ধবিশিষ্ট বৃত্তে ওই চাপ যে পরিমাণ সম্মুখ কোণ উৎপন্ন করে তার ষষ্টিক পরিমাপ নির্ণয় করো।
View Solution[θ=srঅথবা কণ (বৃত্তীয় মানে )=(চাপ)/(ব্যাসার্ধ),সূত্র−সম্পর্কিতপেশ্নাবলি।]দুটিবৃত্তএমনযে,একটিঅপরটিকেন্দ্রবিন্দুগামী।প্রথমবৃত্তেরlদৈর্ঘ্যেরচাপতারকেন্দ্রেthetaএবংদ্বিতীয়বৃত্তেরmদৈর্ঘ্যেরচাপতারকেন্দ্রেphiসম্মুখকোণউৎপন্নকরে।প্রমাণকরােযে,lphi=mtheta।
View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
View Solutionநீள்வட்டம் x216+y2b2=1 மற்றும் அதிபரவளையம் x2144−y281=125 க்கான குவியங்கள் ஒன்றெனில் b2என்பது
View Solutionநேர்க்கோடுகள் x−32=y+54=z−1−13 மற்றும் x+13=y−45=z+22என்பது
View Solutionநேர்க்கோடுகள் x+22=y−3=z−14 மற்றும் x−3a=y−14=z−7a செங்குத்து எனில், (→a) -ன் மதிப்பு
View Solutionபொருத்துக: கோடுகளுக்கு x−14=2−y6=z−412,x−3−2=y−33=5−z6
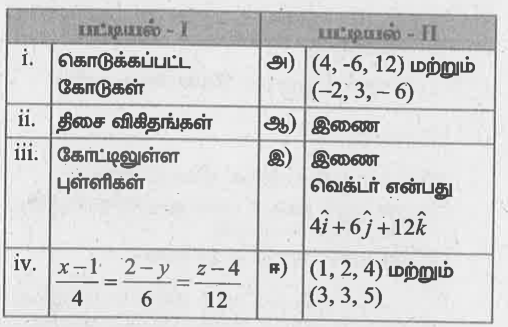
View Solutionx−13=y+12=z−15 மற்றும் x−24=y−13=z+1−2 வெட்டுவதில்லை எனக்காட்டுக.
View Solutionxy=yx+32 হলে , x2y2+y2x2 -এর মান দেখো |
View Solutionx=ab+ba এবং y=ab−ba হলে দেখাও যে, x4+y4−2x2y2=16
View Solutionনীচের সমীকরণটি সমাধান করার চেষ্টা করো : 12(x+1)+13(x+2)+14(x+3)=16
View Solutionxy=yx+32 হলে , x2y2+y2x2 -এর মান দেখো |
View Solution
