An ellipse with semi major axis 'a' semi minor 'b' revolving in uniform magnetic field'B'. Find value of average of joule heating (resistance =R)
To find the average Joule heating in a wire shaped like an ellipse with semi-major axis a and semi-minor axis b revolving in a uniform magnetic field B, we can follow these steps:
1. Understanding the Setup:
- We have an elliptical wire with semi-major axis a and semi-minor axis b.
- The wire is rotating in a uniform magnetic field B.
2. Induced EMF Calculation:
- The magnetic flux Φ through the area of the ellipse is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the ellipse and θ is the angle between the magnetic field and the normal to the area.
- The area A of the ellipse is:
A=πab
- Therefore, the magnetic flux becomes:
Φ=B⋅πab⋅cos(θ)
3. Expressing the Angle:
- As the ellipse rotates, the angle θ changes with time:
θ=ωt
- Substituting this into the flux equation gives:
Φ=B⋅πab⋅cos(ωt)
4. Finding Induced EMF:
- The induced EMF (E) can be calculated using Faraday's law:
E=−dΦdt
- Differentiating the flux:
E=−ddt(B⋅πab⋅cos(ωt))=B⋅πab⋅ωsin(ωt)
5. Current Calculation:
- Using Ohm's law, the current I through the resistance R is:
I=ER=B⋅πab⋅ωsin(ωt)R
6. Calculating Average Joule Heating:
- The Joule heating H over time is given by:
H=I2R⋅t
- Substituting for I:
H=(B⋅πab⋅ωsin(ωt)R)2R⋅t
- This simplifies to:
H=(B⋅πab⋅ω)2sin2(ωt)R⋅t
7. Integrating Over One Complete Cycle:
- To find the average over one complete cycle, integrate from 0 to T (where T=2πω):
Havg=1T∫T0Hdt=1T∫T0(B⋅πab⋅ω)2sin2(ωt)R⋅tdt
- The average value of sin2(ωt) over one complete cycle is 12.
8. Final Expression for Average Joule Heating:
- Thus, the average Joule heating is:
Havg=(B⋅πab⋅ω)22R⋅T
- Substituting T=2πω:
Havg=(B⋅πab⋅ω)22R⋅2πω=(B⋅πab⋅ω)⋅πabBR
Final Result:
Havg=B2⋅π2⋅a2⋅b2⋅ωR
- We have an elliptical wire with semi-major axis a and semi-minor axis b.
- The wire is rotating in a uniform magnetic field B.
- The magnetic flux Φ through the area of the ellipse is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the ellipse and θ is the angle between the magnetic field and the normal to the area.
- The area A of the ellipse is:
A=πab
- Therefore, the magnetic flux becomes:
Φ=B⋅πab⋅cos(θ)
- As the ellipse rotates, the angle θ changes with time:
θ=ωt
- Substituting this into the flux equation gives:
Φ=B⋅πab⋅cos(ωt)
- The induced EMF (E) can be calculated using Faraday's law:
E=−dΦdt
- Differentiating the flux:
E=−ddt(B⋅πab⋅cos(ωt))=B⋅πab⋅ωsin(ωt)
- Using Ohm's law, the current I through the resistance R is:
I=ER=B⋅πab⋅ωsin(ωt)R
- The Joule heating H over time is given by:
H=I2R⋅t
- Substituting for I:
H=(B⋅πab⋅ωsin(ωt)R)2R⋅t
- This simplifies to:
H=(B⋅πab⋅ω)2sin2(ωt)R⋅t
- To find the average over one complete cycle, integrate from 0 to T (where T=2πω):
Havg=1T∫T0Hdt=1T∫T0(B⋅πab⋅ω)2sin2(ωt)R⋅tdt
- The average value of sin2(ωt) over one complete cycle is 12.
- Thus, the average Joule heating is:
Havg=(B⋅πab⋅ω)22R⋅T
- Substituting T=2πω:
Havg=(B⋅πab⋅ω)22R⋅2πω=(B⋅πab⋅ω)⋅πabBR
Havg=B2⋅π2⋅a2⋅b2⋅ωR
Topper's Solved these Questions
Similar Questions
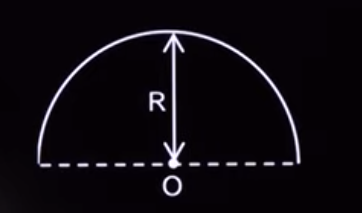
Distance of center of mass from point O by λRπ for uniform semi ring. Find value of λ
View SolutionAn ellipse has semi-major axis of length 2 and semi-minor axis of length 1. It sides between the co-ordinate axes in the first quadrant, while maintaining contact with both x-axis and y-axis.
Q. The locus of the centre of ellipse is :
View Solution
Knowledge Check
An elliptical loop having resistance R, of semi major axis a, and semi minor axis b is placed in a magnetic field as shown in the figure. If the loop is rotated about the x-axis with angular frequency ω, the average power loss in the loop due to Joule heating is :
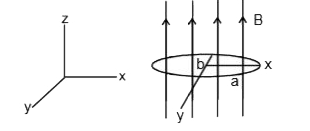 AπabBωRBπ2a2b2B2ω2RCπ2a2b2B2ω22RDzero
AπabBωRBπ2a2b2B2ω2RCπ2a2b2B2ω22RDzeroA liquid is filled into a semi eliiptical cross section with a as semi major axis and b as semi minor axis. The rato of surface tension forces on the curved part and the plane part of the tube in vertical position will be
Aπ(a+b)4bB2πabCπa4bDπ(a−b)4bAn ellipse has semi-major axis of length 2 and semi-minor axis of length 1. It sides between the co-ordinate axes in the first quadrant, while maintaining contact with both x-axis and y-axis.
Q. The locus of the centre of ellipse is :Ax2+y2=3Bx2+y2=5C(x−2)2+(y−1)2=5D(x−2)2+(y−1)2=3
An ellipse has semi-major axis of length 2 and semi-minor axis of length 1. It sides between the co-ordinate axes in the first quadrant, while maintaining contact with both x-axis and y-axis.
Q. The locus of the foci of the ellipse is :
View SolutionAn ellipse has semi-major axis of length 2 and semi-minor axis of length 1. It sides between the co-ordinate axes in the first quadrant, while maintaining contact with both x-axis and y-axis.
Q. The locus of the foci of the ellipse is :
View SolutionAn ellipse has OB as the semi-minor axis, FandF' as its foci, and ∠FBF' a right angle. Then, find the eccentricity of the ellipse.
View SolutionAn ellipse has OB as the semi-minor axis, FandF' as its foci, and ∠FBF' a right angle. Then, find the eccentricity of the ellipse.
View SolutionAn ellipse hase semi-major of length 2 and semi-minor axis of length 1. It slides between the coordinates axes in the first quadrant while mantaining contact with both x-axis and y-axis. The locus of the centre of the ellipse is
View Solution
