Four gases alpha, beta, gamma and delta have KH values 50kbar, 20 kbar, 2xx10^(-3) kbar and 2 kbar respectively. then ?
alpha is more soluble in water
pressure of gamma in 55.5 molal solution is 1 bar
pressure of delta in 55.5 molal solution is 250 bar
pressure of beta in 55.5 molal solution is 50 bar
To solve the problem, we need to analyze the given information about the four gases (alpha, beta, gamma, and delta) and their respective Henry's law constants (K_H). We will evaluate each option one by one based on the principles of Henry's law.
1. Understanding Henry's Law:
Henry's law states that the amount of gas dissolved in a liquid is directly proportional to the partial pressure of that gas above the liquid. Mathematically, it can be expressed as:
P=KH⋅X
where P is the partial pressure of the gas, KH is Henry's law constant, and X is the mole fraction of the gas in the solution.
2. Inversely Proportional Relationship:
Since KH is inversely proportional to the solubility of the gas, a higher KH value indicates lower solubility. Therefore, we can rank the gases based on their KH values:
- Alpha: KH=50kbar (least soluble)
- Beta: KH=20kbar
- Gamma: KH=2×10−3kbar (most soluble)
- Delta: KH=2kbar
3. Evaluating Option 1:
- Option 1 states that "Alpha is more soluble in water."
- Since alpha has the highest KH, it is the least soluble. Thus, this option is incorrect.
4. Evaluating Option 2:
- Option 2 states that "Pressure of gamma in a 55.5 molal solution is 1 bar."
- We calculate the pressure using the formula:
Pgamma=KH⋅Xgamma
- For gamma, KH=2×10−3kbar=2bar (after converting to bar).
- The mole fraction Xgamma for a 55.5 molal solution is approximately 55.51000+55.5≈55.51055.5≈0.0525.
- Thus,
Pgamma=2bar×0.0525≈0.105bar
- Therefore, this option is correct.
5. Evaluating Option 3:
- Option 3 states that "Pressure of delta in a 55.5 molal solution is 250 bar."
- We calculate:
Pdelta=KH⋅Xdelta
- For delta, KH=2kbar=2000bar.
- Using the same mole fraction as above, we find:
Pdelta=2000bar×0.0525≈105bar
- Thus, this option is incorrect.
6. Evaluating Option 4:
- Option 4 states that "Pressure of beta in a 55.5 molal solution is 50 bar."
- We calculate:
Pbeta=KH⋅Xbeta
- For beta, KH=20kbar=20000bar.
- Using the same mole fraction:
Pbeta=20000bar×0.0525≈1050bar
- Thus, this option is also incorrect.
Conclusion:
The only correct option is Option 2: "Pressure of gamma in a 55.5 molal solution is 1 bar."
Henry's law states that the amount of gas dissolved in a liquid is directly proportional to the partial pressure of that gas above the liquid. Mathematically, it can be expressed as:
P=KH⋅X
where P is the partial pressure of the gas, KH is Henry's law constant, and X is the mole fraction of the gas in the solution.
Since KH is inversely proportional to the solubility of the gas, a higher KH value indicates lower solubility. Therefore, we can rank the gases based on their KH values:
- Alpha: KH=50kbar (least soluble)
- Beta: KH=20kbar
- Gamma: KH=2×10−3kbar (most soluble)
- Delta: KH=2kbar
- Option 1 states that "Alpha is more soluble in water."
- Since alpha has the highest KH, it is the least soluble. Thus, this option is incorrect.
- Option 2 states that "Pressure of gamma in a 55.5 molal solution is 1 bar."
- We calculate the pressure using the formula:
Pgamma=KH⋅Xgamma
- For gamma, KH=2×10−3kbar=2bar (after converting to bar).
- The mole fraction Xgamma for a 55.5 molal solution is approximately 55.51000+55.5≈55.51055.5≈0.0525.
- Thus,
Pgamma=2bar×0.0525≈0.105bar
- Therefore, this option is correct.
- Option 3 states that "Pressure of delta in a 55.5 molal solution is 250 bar."
- We calculate:
Pdelta=KH⋅Xdelta
- For delta, KH=2kbar=2000bar.
- Using the same mole fraction as above, we find:
Pdelta=2000bar×0.0525≈105bar
- Thus, this option is incorrect.
- Option 4 states that "Pressure of beta in a 55.5 molal solution is 50 bar."
- We calculate:
Pbeta=KH⋅Xbeta
- For beta, KH=20kbar=20000bar.
- Using the same mole fraction:
Pbeta=20000bar×0.0525≈1050bar
- Thus, this option is also incorrect.
The only correct option is Option 2: "Pressure of gamma in a 55.5 molal solution is 1 bar."
Similar Questions
If the two quadratic ax2+bx+c=0 and lx2+mx+n=0 have roots α,β and γ,δrespectively. If α,β,γ and δ are in A.P and Δ1 and Δ2 be the discriminants of these quadratics then Δ1Δ2 is
View SolutionIf α,β,γ,δ are the roots of the equation x4−Kx3+Kx2+Lx+m=0,whereK,L,andM are real numbers, then the minimum value of α2+β2+γ2+δ2 is 0 b. −1 c. 1 d. 2
View Solution
Knowledge Check
Henry’s constant (in kbar) for four gases α,β,γandδ in water at 298 K is given below :

(density of water = 103 kg m−3 at 298 K)
This table implies that :Asolubility of γ at 308 K is lower than at 298 KBThe pressure of a 55.5 molal solution of δ is 250 barCα has the highest solubility in water at a given pressureDThe pressure of a 55.5 molal solutio of γ is 1 barFor the solution of the gases W,X,Y and z in water at 298 K , the Henrys law constants (KH) are 0.5, 2, 35 and 40 kbar, respectively. The correct plot for the given data is :
A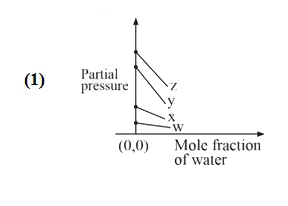 B
B C
C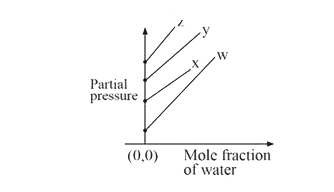 D
D
If α,β are the roots of ax2+bx+c=0andα+k,β+k are the roots of px2+qx+r=0, then k=
A-2,-32B−2,3C−6,3D−6,−32
Let αandβ be the roots of x2−x+p=0andγandδ be the root of x2−4x+q=0. If α,β,andγ,δ are in G.P., then the integral values of pandq , respectively, are −2,−32 b. −2,3 c. −6,3 d. −6,−32
View SolutionLet α,β be the roots of x2−x+p=0 and γ,δ are roots of x2−4x+q=0. If α, β, γ, δ are in G.P., then the integral value of p and q, respectively, are −2,−32 b. −2,3 c. −6,3 d. −6,−32
View SolutionIf α,β,γandδ are the roots of the equation x4−bx−3=0, then an equation whose roots are α+β+γδ2,α+β+δγ2,α+δ+γβ2,andδ+β+γα2, is:
View SolutionIf α,β,γ,δ be four angles of a cyclic quadrilateral taken in clockwise direction then the value of (2+Σcosαcosβ) will be:
View Solutionα,β,γandδ are the smallest positive angle in ascending order of magnitude which have their sines equal to the positive quantity k. The value of 4sinα2+3sinβ2+2sinγ2+sinδ2 is equal to
View Solution
