A तथा B के बीच अभिक्रिया के लिए निम्न तथ्य दिये गये हैं
गणना कीजिए
(i) क्रमश: A तथा B के सापेक्ष अभिक्रिया की कोटि।
(ii) 300 K पर वेग स्थिरांक।
(iii) सक्रियण ऊर्जा तथा
(iv) पूर्व चरघातांकी गुणांक (pre-exponential factor)।
(i) माना A तथा B के बीच अभिक्रिया के लिए वेग नियम निम्न है
dxdt=k[A]m[B]n
300 K पर प्रथम तथ्यों के लिए,
5×10−4=k[2.5×10−4]m[3.0×10−5]n….......(i)
4×10−3=k[5×10−4]m[6×10−5]n….......(ii)
1.6×10−2=k[1×10−3]m[6.0×10−5]n….......(iii)
समी (ii) व (ii) से, 1.6×10−24×10−3=[1×10−35.0×10−4]xx[6×10−56×10−5]
अथवा 4 = (2)m
∴22=2m "अथवा" m=2
समी (i) व (ii) से,
4×10−35×10−4 = [1.0×10−35.0×10−4]m×[6×10−53×10−5]n
8 = 2m×2n
8=22×2n
2=2n
∴ n=1
अत: A तथा B के सापेक्ष अभिक्रिया की कोटि क्रमश: 2 तथा 1 होगी।
dxdt=k[A]2[B]
300 K पर प्रथम तथ्यों से,
5.0×10−4 = k300[2.5×10−4][3.0×10−5]
∴ k300=2.66×108ली2मोल−2से−1
320 K पर प्रथम तथ्यों से,
2.0×10−3=k320[2.5×10−4^(2)[3.0×10−5]
∴ k320=1.07×109ली2मोल−2से−−1 हम जानते हैं कि
(iii) सक्रियण ऊर्जा (Ea) = 2.303RT1T2T2−T1log10k320k300
2.303×8.314×300×320320−300log10(1.07×109)2.66×108जूल
55.56×103 जूल (क्योंकि R का मान जूल में है)
(iv) आरहेनियस समीकरण से,
k = Ae−Ea/RT
300K पर,
2.66×108=Ae−55.56×1038.314×300
अथवा loge2.66×108=logeA−55.56×1038.314×300
अथवा 2.303×log10A−55.56×1038.314×300
इस समीकरण को हल करने पर,
A = 1.25×1018
Topper's Solved these Questions
- रासायनिक बलगतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - रासायनिक बलगतिकी EXERCISE - पूर्णांक उत्तर प्रकार
2 Videos
- रासायनिक एवं आयनिक साम्यावस्था BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - रासायनिक एवं आयनिक साम्यावस्था EXERCISE - विश्लेषणात्मक प्रश्न
35 Videos
- रेडॉक्स अभिक्रियाएँ एवं विधुत रसायन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - रेडॉक्स अभिक्रियाएँ एवं विधुत रसायन EXERCISE - विश्लेषणात्मक प्रश्न
35 Videos
Similar Questions
भिक्रिया R → Pमें, R की सान्द्रता समय के फलन में मापी गयी, और निम्न आंकड़े पाए गए
अभिक्रिया की कोटि है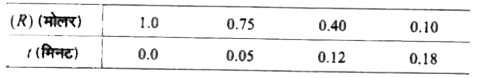
View Solutionएक दुर्बल अम्ल HA का वियोजन स्थिरांक 4.9×10−8 है। आवश्यक सन्निकटनों (approximations) के बाद निम्न की गणना कीजिए।
(i) प्रतिशत आयनन (ii) pH मान (iii) अम्ल के डेसीमोलर विलयन में OH की सान्द्रता (जल का pH मान 7 है।)
View Solutionएक विधुत अपघटन (electrolysis) के प्रयोग में, श्रेणी में जुड़ी हुई दो सेलों के मध्य 5 घण्टे के लिए धारा प्रवाहित की गयी | प्रथम सेल में सोने का विलयन है जबकि दूसरी सेल में कॉपर सल्फेट का विलयन है | प्रथम सेल में 9.85 ग्राम सोना एकत्रित हुआ | यदि सोने की ऑक्सीकरण संख्या +3 है, तो दूसरी सेल के कैथोड पर निक्षेपित (deposit) होने वाले कॉपर की मात्रा ज्ञात कीजिए | प्रवाहित धारा के मान की एम्पियर में गणना कीजिए | (Au का परमाणु भार = 197, तथा Cu का परमाणु भार = 63.5)
View Solutionअभिक्रिया (A+B)→उत्पाद के लिये निम्न आँकड़े प्राप्त हुए |
इन आँकड़ों से A एवं B के सन्दर्भ में अभिक्रिया की कोटि तथा सम्पूर्ण अभिक्रिया की कोटि का निर्धारण कीजिए।
View Solutionअभिक्रिया की दर को प्रभावित करने वाले कारक|वेग नियम तथा वेग स्थिरांक
View Solutionरसायनिक अभिक्रियाओं के प्रकार | संयोजन अभिक्रिया तथा उदाहरण | वियोजन अभिक्रिया तथा उदाहरण | विस्थापन अभिक्रिया तथा उसके उदाहरण | दिविस्थापन अभिक्रिया तथा उसके उदाहरण
View Solutionऊर्जा तथा ऊर्जा के रूप
View Solutionकार्य तथा कार्य के प्रकार#!#ऊर्जा तथा ऊर्जा के प्रकार
View SolutionRevision|अभिक्रिया के वेग पर ताप का प्रभाव|पूर्वचरघातांकी गुणांक|संक्रियण ऊर्जा|Summary
View Solutionप्रथम तथा द्वितीय कोटि की अभिक्रिया पर आधारित प्रश्न
View Solutionमेथिल नाइट्राइट और एथिल नाइट्राइट के लिए अपघटन की दर के दर स्थिरांक क्रमश k_1 और k_2 के पदों में दिए जा सकते हैं। दोनों अभिक्रियाओं के लिए सक्रियण ऊर्जा क्रमश: 152.30kJ mol^(-1) और 157.7kJ mol^(-1) है और मेथिल नाइट्राइट और एथिल नाइट्राइट के अपघटन के लिए आवृत्ति गुणांक क्रमशः 10^13 और 10^14 हैं। उस ताप की गणना कीजिए जिस पर दोनों अभिक्रियाओं के लिए दर स्थिरांक समान होगा।
View Solutionएक अभिक्रिया के लिए सक्रियण ऊर्जा 100 kJ mol^(-1) है। उत्प्रेरक की उपस्थिति सक्रियण ऊर्जा को 75% कम करती है। 20^(@)C पर अभिक्रिया की दर पर क्या प्रभाव होगा, यदि अन्य परिस्थितियाँ समान हैं?
View Solutionएक ऊष्माक्षेपी अभिक्रिया, A→B की सक्रियण ऊर्जा 15kcalmol−1 है और अभिक्रिया की ऊर्जा 5kcalmol−1 है। अभिक्रिया B→A के लिए सक्रियण ऊर्जा kcalmol−1 में होगी-
View Solutionनिम्न "log" t_(50%) तथा log सांद्रता (a) के मध्य वक्र वाले रासायनिक परिवर्तन के लिए अभिक्रिया की कोटि और दर स्थिरांक क्या होगा?
View Solutionसक्रियण ऊर्जा की गणना के लिए log k बनाम 1/T के बीच का आरेख किसके द्वारा दिखाया गया है?
View Solution227∘C पर अभिक्रिया के साम्य स्थिरांक के मान की गणना कीजिए, यदि अभिक्रिया X+Y⇔Z के लिए ΔG∘−4.606 kcal है।
(R=2.0cal. mol−1K−1)
View Solution
