रेखाओं ax+by+c का समुच्चय , जहाँ 3a+2b+4c=0 बिन्दु ............... पर संगामी हैं।
The correct Answer is:(34,12)
Step by step video, text & image solution for रेखाओं ax+by+c का समुच्चय , जहाँ 3a+2b+4c=0 बिन्दु ............... पर संगामी हैं। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सरल रेखा BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल रेखा EXERCISE - सत्य/असत्य
4 Videos
- सरल रेखा BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल रेखा EXERCISE - मैट्रिक्स -सुमेल प्रकार (नीचे दिए गए प्रश्न में दो स्तम्भों में कथन दिए गए हैं। जिनका सुमेल करना है। स्तम्भ I में दिए गए कथनों को A , B , C व D से तथा स्तम्भ II में कथनों को p , q , r व s से नामांकित किया गया है। इस प्रश्न का उत्तर दीजिए
1 Videos
- सरल रेखा BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल रेखा EXERCISE - बहुविकल्पीय प्रश्न II ( एक से अधिक विकल्प सही है )
2 Videos
- सम्मिश्र संख्याएँBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सम्मिश्र संख्याएँEXERCISE - एकल पूर्णांक प्रश्न
3 Videos
- सरल रेखायुग्म BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल रेखायुग्म EXERCISE - विश्लेषणात्मक प्रश्न
1 Videos
Similar Questions
सरल रेखा 5x+4y=0, सरल रेखाओं x+2y−10=0 और 2x+y+5=0 के प्रतिच्छेद बिन्दु से होकर जाती है ।
View Solutionमाना रेखाओं के समीकरण
L1:x+3y−5=0,L2:3x−ky−1=0
तथा L3:5x+2y−12=0 हैं।
स्तम्भ I में कथन/व्यंजक को स्तम्भ II के कथन/ व्यंजक से सुमेल कीजिए।
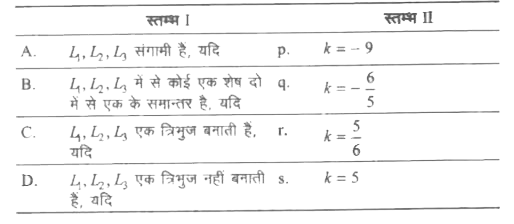
View Solutionतीन रेखाएँ px+qy+r=0,qx+ry+p=0 और rx+py+q=0 संगामी होंगी, यदि
View Solutionमान लीजिए कि z कोई सम्मिश्र संख्या (complex number) है जिसके लिए |z−3−2i|≤2 सत्य है, तो |2z−6+5i| का न्यूनतम मान है _______
View Solutionप्रदर्शित करें कि वक्र 3x2+3y2−2x+4y=0 की सभी जीवायें जो कि मूल बिन्दु पर समकोण अन्तरित करती है, संगामी होती है। संगमन बिन्दु भी ज्ञात कीजिए।
View SolutionThe set of lines ax+by+c=0, where 3a+2b+4c=0, is concurrent at the point:
View SolutionIf a,b,c are variables such that 3a+2b+4c=0 , then show that the family of lines givenby ax+by+c=0 pass through a fixed point. Also, find that point.
View SolutionIf both roots of the equation ax2+x+c−a=0 are imaginary and c>−1, then a.3a>2+4c b.3a<2+4c c.c<a d. none of these
View Solution(1) if a+b+c=0 the straight line 2ax+3by+4c=0 passes through the fixed point (2) if 3a+2b+4c=0 the straight line ax+by+c=0 passes through the fixed point
View SolutionThe lines ax+by+c=0, where 3a+2b+4c=0, are concurrent at the point 31132'4
View SolutionThe set of lines ax+by+c=0, where 3a+2b+4c=0 is concurrent at the point…
View SolutionFor any real values of a,b,c such that 3a, +2b+4c=0, line ax+by+c=0 passes through the fixed point whose coordinates are
View SolutionIf 3a+2b+4c=0 then the lines ax+by+c=0 pass through the fixed point
View SolutionIf 3a+2b+4c=0 then the lines ax+by+c=0 pass through the fixed point
View SolutionThe set of lines ax + by + c = 0 where 3a + 2b + 4c = 0 intersect at the point
View Solution
