माना कि परवलय (parabola) y2=4x पर P एक ऐसा बिन्दु है जो वृत्त x2+y2−4x−16y+64=0 के केन्द्र बिन्दु S से न्यूनतम दूरी पर है | माना कि वृत्त पर बिन्दु Q ऐसा है कि वह रेखाखंड SP को आंतरिक विभाजित करता है | तब
SP=2√5
SQ:QP=(√5+1):2
परवलय के बिंदु P पर अभिलम्ब का x- अंत: खंड है
वृत्त के बिंदु Q पर स्पर्श रेखा की ढाल 12 है
The correct Answer is:A, C, D
y2=4x के बिंदु (t2,2t) पर स्पर्श रेखा निम्न है 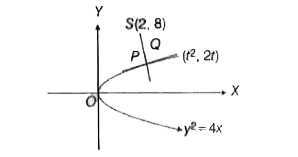
y(2t)=2(x+t2)
⇒yt=x+t2......(i)
P(t2,2t) पर अभिलम्ब का समीकरण निम्न है
y+tx=2t+t3
चुकी P पर अभिलम्ब, वृत्त के केंद्र S(2,8) से होकर जाता है
8+2t=2t+t3
⇒t=2 अर्थार्त P(4,4)
[चुकी दो वक्रो के बिच की न्यूनतम दुरी उनके उभयनिष्ट अभिलम्ब के सापेक्ष होती है और उभयनिष्ट अभिलम्ब, वृत्त के केंद्र से होकर जाता है]
∴SP=√(4−2)2+(4−8)2=2√5
अंत: विकल्प (a) सत्य है
साथ ही, SQ=2
PQ=SP−SQ=2√5−2
इस प्रकार SQQP=1√5−1=√5+14
अंत: विकल्प (b) असत्य है
अब अभिलम्ब का x- अंत: खंड x=2+22=6 है
अंत: विकल्प (c) सत्य है
−1t=12
अंत: विकल्प (d) सत्य है
Topper's Solved these Questions
- परवलयBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - रिक्त स्थानों की पूर्ति कीजिये
1 Videos
- परवलयBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - श्रृंख्लाबद्ध बोधन प्रकार
4 Videos
- परवलयBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - एकल पूर्णांक प्रश्न
5 Videos
- निश्चित समाकलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - एकल पूर्णाक प्रश्न
7 Videos
- प्रतिलोम वृत्तीय फलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रतिलोम वृत्तीय फलन EXERCISE - एकल पूर्णांक प्रश्न
1 Videos
Similar Questions
परवलय y2=4x के नाभिलम्ब (latusrectum) के सिरों पर खींची गयी स्पर्शी का प्रतिछेद बिंदु .............है
View Solutionमाना कि PQ परवलय y2=4ax की एक नाभीय जीवा है। बिन्दुओं P तथा Q पर परवलय की स्पर्श रेखाएँ एक बिन्दु पर मिलती है जोकि रेखा y=2x+a,a>0 पर स्थित है।
जीवा PQ की लम्बाई है।
View Solutiony2=8x एक परवलय है। मान लीजिए एक त्रिभुज का क्षेत्रफल है जो नाभिलम्ब जीवा के सिरों और परवलय के बिन्दु P(12,2) द्वारा निर्मित है और Δ2 उस त्रिभुज का क्षेत्रफल है, जो बिन्दु P पर और नाभिलम्ब जीवा के सिरों पर खींची गई स्पर्शियों द्वारा बना है। तब Δ1Δ2 है।
View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
View Solutionमाना f:[0,4π]→[0,π],f(x)=cos−1(cosx) के द्वारा परिभाषित है। तब x∈[0,4π] में समीकरण f(x)=10−x10 को संतुष्ट करने वाले बिंदुओं की संख्या है
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionमाना PQ और RS,r त्रिज्या के वृत्त के व्यास के सिरों पर खींची गई स्पर्शियाँ है। यदि PS और RQ परिधि पर स्थिति बिन्दु X पर प्रतिच्छेद करते है तो 2r बराबर है-
View Solutionयदि वृत्त x2+y+6x+6y=2 के बिन्दु P पर खींची गई स्पर्शी सरल रेखा 5x−2y+6=0 से y-अक्ष के बिन्दु Q पर मिलती है, तो PQ की लम्बाई है
View Solutionबिन्दु (-1,0) से होकर जाने वाले और y-अक्ष को (0,2) पर स्पर्श करने वाला वृत्त निम्न बिन्दु से भी होकर जाता है ।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionपरवलय y2=36x पर स्थित वे बिन्दु जिनकी कोटि भुज की तिगुनी है, हैं
View Solution
