परवलय y2=4x के शीर्ष O से दो जीवायें OP और OQ खींची जाती हैं, जो एक-दूसरे से समकोण बनाती हैं। दिखाइए कि P की सभी स्थितियों के लिए PQ, परवलय के अक्ष को एक नियत बिन्दु पर काटता है। PQ के मध्य-बिन्दु का बिन्दुपथ ज्ञात कीजिए।
The correct Answer is:{2(m2+1m2),2(1m−m)}
माना जीवा OP का समीकरण y=mx है
तो जीवा OQ का समीकरण y=−1mx होगा।
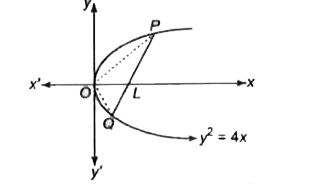
y=mx और y2=4x का प्रतिछेद बिंदु P(4m2,4m) है
y=−1mx और y2=4x का प्रतिछेद बिंदु Q(4m2,−4m) है PQ का समीकरण
y=4m=4m+4m4m2−4m2(x−4m2)
⇒y+4m=m1−m2(x−4m2)
⇒(1−m2)y+4m−4m3=mx−4m3
⇒mx−(1−m2)y−4m=0
यह रेखा x-अक्ष से मिलती है, जहाँ y=0
अर्थार्त x=4⇒OL=4, जो एक अचर है, क्योकि यह से स्वतंत्र है
पुनः माना (h,k) PQ का मध्य बिंदु है तो
h=4m2+4m22 और k=4m−4m2
⇒h=2(m2+1m) और k=2(1m−m)
⇒h=2[(m−1m))2+2] और k=2(1m−m)
m का विलोपन करने पर, 2h=k2+8
y2=2(x−4), बिन्दुपथ का अभीष्ट समीकरण है
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - एकल पूर्णांक प्रश्न5videos
परवलय
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - दृढ़कथन-कारण प्रकार2videos
परवलय
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - एकल पूर्णाक प्रश्न7videos
निश्चित समाकलन
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रतिलोम वृत्तीय फलन EXERCISE - एकल पूर्णांक प्रश्न1videos
प्रतिलोम वृत्तीय फलन
Similar Questions
y2=8x एक परवलय है। मान लीजिए एक त्रिभुज का क्षेत्रफल है जो नाभिलम्ब जीवा के सिरों और परवलय के बिन्दु P(12,2) द्वारा निर्मित है और Δ2 उस त्रिभुज का क्षेत्रफल है, जो बिन्दु P पर और नाभिलम्ब जीवा के सिरों पर खींची गई स्पर्शियों द्वारा बना है। तब Δ1Δ2 है।
05:19View Solutionप्रत्येक प्रश्न में वक्तव्य I(कथन ) और वक्तव्य II (कारण) दिए गए हैं। प्रश्न में चार विकल्प (a), (b), (c) तथा (d) है , जिनमें से केवल एक सही है।
वक्तव्य I वक्र y=−x22+x+1 रेखा x=1 के परितः सममित (symmectric) है
क्योंकि
वक्तव्य II परवलय अपने अक्ष के परित: सममित है।04:29View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
04:21View Solutionमाना f:[0,4π]→[0,π],f(x)=cos−1(cosx) के द्वारा परिभाषित है। तब x∈[0,4π] में समीकरण f(x)=10−x10 को संतुष्ट करने वाले बिंदुओं की संख्या है
02:13View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
03:57View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
06:40View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
01:50View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
04:32View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
04:45View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
03:50View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
04:26View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
02:50View Solutionएक परवलय का अक्ष X-अक्ष के अनुदिश है। यदि इसके शीर्ष तथा नाम नाभि , X-अक्ष कि धनात्मक दिशा में मूलबिंदु से क्रमशः 2 तथा 4 कि दुरी पर हैं , तो इनमें से कौन - सा बिन्दु इस परवलय पर स्थित नहीं है ?
03:40View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
02:57View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
03:08View Solutionपरवलय y2=4ax की, उन जीवाओं के मध्य बिन्दुओं का बिन्दुपथ जो मूल बिन्दु से होकर जाती हैं, होगा
03:33View Solution

