यदि सभी स्वतंत्र राशियों की मापन त्रुटियाँ ज्ञात हो, तो किसी निर्भर राशि की त्रुटि का परिकलन किया जा सकता है। इस परिकलन में श्रेणी प्रसार का प्रयोग किया जाता है और इस प्रसार में त्रुटि के पहले घात पर रुण्डित किया जाता है। उदाहरणस्वरूप , सम्बन्ध में यदि , और की त्रुटियाँ क्रमश : , और हो, तो
का श्रेणी प्रसार , में पहले घात तक, है। स्वतंत्र राशियों की आपेक्षिक त्रुटियाँ सदैव जोड़ी जाती है। इसलिए की त्रुटि होगी।
उपरोक्त परिकलन में , माने गए है। इसलिए इन राशियों की उच्चतर घाते उपेक्षित है।
एक विमा रहित राशि को मापकर , एक अनुपात का परिकलन करना है। यदि की मापन की त्रुटि है , तो के परिकलन की त्रुटि क्या होगी ?
The correct Answer is:B
अवकलन करने पर
हम लिख सकते है ,
या
Topper's Solved these Questions
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर 2-खण्ड 1
6 Videos
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर 2-खण्ड 2
8 Videos
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर 1-खण्ड 2
8 Videos
- सॉल्वड पेपर 2017 JEE MAIN संयुक्त प्रवेश परीक्षा BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर 2017 JEE MAIN संयुक्त प्रवेश परीक्षा EXERCISE - MCQs
30 Videos
- सॉल्वड पेपर्स 2020BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2020EXERCISE - PHYSICS
36 Videos
Similar Questions
द्रव्यमान m का एक कण शुरुआत में मूल बिन्दु पर विरामावस्था में है। कण पर एक बल लगाने से वह x-अक्ष पर चलने लगता है और कण की गतिज ऊर्जा K, समय के साथ dKdt=γt के अनुसार परिवर्तित होती है, जहाँ γ एक उचित विमाओ वाला धनात्मक नियतांक है। निम्नलिखित कथनो में से कौन-सा (से) सही है (है )?
View Solutionएक ठोस क्षैतिज तल तेल के एक पतली परत से ढका हुआ है। द्रव्यमान m=0.4kg का एक आयताकार गुटका इस तल पर विरामावस्था में है। 1.0 न्यूटन से परिमाण का एक आवेग गुटके पर t=0 समय पर लगया जाता है जिसके फलस्वरूप गुटका x-अक्ष पर v(t)=v0e−t/τ वेग से चलने लगता है, जहाँ v0 एक स्थिर राशि है और τ=4 सेकण्ड है। समय t=τ पर गुटके का विस्थापन ................... मीटर है | e−1=0.37 ले
View SolutionA और B दो सदिश राशियाँ है, जहाँ A=aˆi और B=a(cosωˆi+sinωˆj) है। यहाँ a एक स्थिरांक है और ω=π6rads−1 है। यदि |A+B|=√3|A−B| प्रथम बार समय t=τ पर होता है , तो τ का मान सेकण्ड में ,........ है।
View Solutionएक प्रेक्षक प्रकाश गति की आधी गति से 10GHz आवृत्ति के एक स्थिर सूक्ष्म तरंग स्रोत की तरफ जा रहा है। प्रेक्षक द्वारा मापी गयी सूक्ष्म तरंग की आवृत्ति का मान होगा। (प्रकाश की चाल =3×108ms−1)
View Solutionक्षैतिज अवस्था में रखे हुए एक तख्ने (plank) में एक छिद्र है जिसकी त्रिज्या r है। तख्ते के इस छिद्र पर एक R(R>r) त्रिज्या वाले फुटबॉल को रखा गया है। जैसा कि नीचे चित्र में दिखाया गया है, इस तख्ते को अब एक छोर से ऊपर उठाया जाता है जिससे कि यह उन्नत हो कर क्षितिज से θ का कोण बनाता है। θ का अधिकतम मान जब तक कि फुटबॉल तख्ते पर लोटना प्रारंभ नहीं करती है, इस तरह है कि [चित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है]
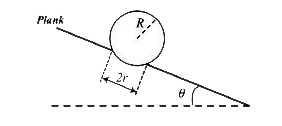
View SolutionIfy=x4+x3+x2+x+1,x=1,δx=0.02, then δy≈....
View SolutionIf the measurement errors of all the independent zodiacs are known, then the error of a dependent sum can be calculated. In this calculation, range propagation is used and this spread is truncated to the first power of the error. For example, relationship z=x//y In if the errors of x, y and z respectively Deltax, Deltay And Deltaz If so z pm Deltaz=(x+Deltax)/(y pm Deltay)=(x)/(y)(1pm (Deltax)/(x))(1pm (Deltay)/(y))^(-1) . (1pm (Deltay)/(y))^(-1) Range of, Deltay//y Until the first power, 1pm (Deltay//y) Is Relative errors of independent sums are always added. Hence z will be the error Deltaz=z((Deltax)/(x)+(Deltay)/(y)) . In the above calculation (Deltax)/(x) lt lt 1, (Deltay)/(y) lt lt 1 Are considered Hence the higher powers of these zodiac signs are neglected. An unbounded amount alpha By measuring, a ratio r=(( 1 - a ))/((1+a)) Has to be calculated. If alpha Measurement error of Deltaa is (Deltaa//altlt1) Then error of r calculation Deltar What will happen
View SolutionIf the measurement errors of all the independent zodiacs are known, then the error of a dependent sum can be calculated. In this calculation, range propagation is used and this spread is truncated to the first power of the error. For example, relationship z=x//y In if the errors of x, y and z respectively Deltax, Deltay And Deltaz If so z pm Deltaz=(x+Deltax)/(y pm Deltay)=(x)/(y)(1pm (Deltax)/(x))(1pm (Deltay)/(y))^(-1) . (1pm (Deltay)/(y))^(-1) Range of, Deltay//y Until the first power, 1pm (Deltay//y) Is Relative errors of independent sums are always added. Hence z will be the error Deltaz=z((Deltax)/(x)+(Deltay)/(y)) . In the above calculation (Deltax)/(x) lt lt 1, (Deltay)/(y) lt lt 1 Are considered Hence the higher powers of these zodiac signs are neglected. The number of radioactive nuclei at the start of an experiment is 3000. In first 1.0 seconds of use 1000 +- 40 Nuclei are lost. If |x|ltlt1 If, to the first power of x, in ( 1 + x ) = x Is Error in scoring Deltalambda, s^(-1) I have
View SolutionIf U=ln(x3+y3+z3−3xyz), show that δuδx+δuδy+δuδz=3x+y+z
View SolutionFind Δy and dy for the function y=x2+x, when x=10, Δx=0.1
View SolutionFind Δyanddy for the following functions for the values of x and Δx which are shown against each of the functions.
y=cos(x),x=60∘andΔx=1∘
View SolutionThe ratio of the monthly income of X and Y is 5 : 4 and that of their monthly expenditure is 9 : 7 . If the income of Y is equal to the expenditure of X, then what is the ratio of the saving of X and Y?
X और Y की मासिक आय का अनुपात 5: 4 है और उनके मासिक खर्च का अनुपात 9: 7 है। यदि Y की आय X के व्यय के बराबर है, तो X और Y की बचत का अनुपात कया है?
View SolutionA and B are solutions of acid and water. The ratios of water and acid in A and B are 4 : 5 and 1 : 2, respectively If x liters of A is mixed with Y liters of B, then the ratio of water and acid in themixture becomes 8 : 13. What is x : y ?
A और B एिसड और पानी के मिश्रण हैं। A और B में पानी और एसिड का अनुपात क्रमशः 4: 5 और 1: 2 है, यदि x लीटर A को Y लीटर B के साथ मिलाया जाता है, तो मिश्रण में पानी और एसिड का अनुपात 8: 13 हो जाता है। तो x : y ज्ञात कीजिए ।
View SolutionIf x% of y is 150 and y% of z is 300, then the relation between x and z is :
यदि y का x% 150 है और z का y% 300 है, तो x और z में क्या संबंध है ?
View Solutionहाइड्रोजन के तीन समस्थानिक (A), (B) और (C) है | यदि (A), (B) और (C) में न्यूट्रोनो की संख्या क्रमश: (x), (y) और (z) है, तो (x), (y) और (z) का योग होगा-
View Solutionबोरेक्स में बोरॉन-ऑक्सीजन बंधों की कुल संख्या 'x' है और बोरॉन ऑक्सीजन-बोरॉन बंधों की 'y' है। तो x - y का मान है:
View Solution
