अनुनादी वायु-स्तम्भ के एक प्रयोग में ध्वनि की चाल मापने के लिए 500 हर्ट्ज की आवृति वाले एक स्वरित्र द्विभुज का उपयोग किया जाता है। अनुनाद नली में जल का स्तर बदलकर वायु-स्तम्भ की लम्बाई बदली जाती है। दो उत्तरोत्तर अनुनाद वायु-स्तम्भ की लम्बाई 50.7 सेमी और 83.9 सेमी पर सुने जाते है। निम्लिखित कथनो में से कौन-सा (से) सही है (है ) ?
इस प्रयोग में निर्धारित ध्वनि की चाल 332 मी/से−1 है
इस प्रयोग में अत्यं संशोधन 0.9 सेमी है
ध्वनि तरंग की तरंगदैर्ध्य 66.4 सेमी है
50.7 सेमी पर सुने जाने वाला अनुनाद , मूल गुणावृत्ति है
The correct Answer is:A:B:C
माना nवी गुणावृत्ति 50.7 सेमी पर है और (n+1)वी गुणावृत्ति 83.9 सेमी पर है
∴ इनका अन्तर λ/2 है
∴λ2=(839−50.7) सेमी या λ=66.4 सेमी
∴λ4=16.6 सेमी
मुख्य सनादी की लम्बाई λ/4 और 50.7 सेमी के समीपस्थ होगी या इसके विषम गुणक में होगी।
16.6×3=49.8 सेमी, इसलिए 50.7, तीसरी गुणावृत्ति है। यदि अन्त्य संशोधन e है, तब e+50.7=3λ4
e=49.8−50.7=−0.9सेमी
∴ ध्वनि की चाल , v=fλ
v=500×66.4=332m/s
Topper's Solved these Questions
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर 2-खण्ड 2
8 Videos
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर 2-खण्ड 3
4 Videos
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर 1-खण्ड 3
4 Videos
- सॉल्वड पेपर 2017 JEE MAIN संयुक्त प्रवेश परीक्षा BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर 2017 JEE MAIN संयुक्त प्रवेश परीक्षा EXERCISE - MCQs
30 Videos
- सॉल्वड पेपर्स 2020BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2020EXERCISE - PHYSICS
36 Videos
Similar Questions
एक ठोस क्षैतिज तल तेल के एक पतली परत से ढका हुआ है। द्रव्यमान m=0.4kg का एक आयताकार गुटका इस तल पर विरामावस्था में है। 1.0 न्यूटन से परिमाण का एक आवेग गुटके पर t=0 समय पर लगया जाता है जिसके फलस्वरूप गुटका x-अक्ष पर v(t)=v0e−t/τ वेग से चलने लगता है, जहाँ v0 एक स्थिर राशि है और τ=4 सेकण्ड है। समय t=τ पर गुटके का विस्थापन ................... मीटर है | e−1=0.37 ले
View Solutionविभिन्न आवेश वितरणों से उत्पन्न होने वाले विधुत क्षेत्र E का एक बिन्दु P(0,0,d) और मापन किया जाता है और इस विधुत क्षेत्र E की d पर निर्भरता अलग-अलग पायी जाती है सूची I में E और d के बीच में अलग-अलग सम्बन्ध दिए गए है। सूची II विभिन्न प्रकार के आवेश वितरणों और उनके स्थानों को बताती है। सूची I के फलनों का सूची II से सम्बन्धित आवेश वितरणों से सुमेल कीजिए।


View Solutionविधुतचुम्बकीय सिद्धांत के अनुसार,विधुत और चुम्बकीय परिघटनाओं के बीच सम्बन्ध होता है। इसलिए विधुत और चुम्बकीय राशियों के विमाओ में भी सम्बन्ध होने चाहिए। निम्नलिखित प्रश्नो में [E] और [B] क्रमश : विधुत और चुम्बकीय क्षेत्रो की विमाओ की दर्शाते है, जबकि [ε0] और [μ0] क्रमश : मुक्त आकाश की परा वैधुताक और चुम्बकशीलता की विमाओ को दर्शाते है [L] और [T] क्रमश : लम्बाई और समय की विमाएँ है। सभी राशियों SI मात्रको में दी गई है।
[E] और [B] के बीच में सम्बन्ध है
View Solutionएक प्रेक्षक प्रकाश गति की आधी गति से 10GHz आवृत्ति के एक स्थिर सूक्ष्म तरंग स्रोत की तरफ जा रहा है। प्रेक्षक द्वारा मापी गयी सूक्ष्म तरंग की आवृत्ति का मान होगा। (प्रकाश की चाल =3×108ms−1)
View Solutionक्षैतिज अवस्था में रखे हुए एक तख्ने (plank) में एक छिद्र है जिसकी त्रिज्या r है। तख्ते के इस छिद्र पर एक R(R>r) त्रिज्या वाले फुटबॉल को रखा गया है। जैसा कि नीचे चित्र में दिखाया गया है, इस तख्ते को अब एक छोर से ऊपर उठाया जाता है जिससे कि यह उन्नत हो कर क्षितिज से θ का कोण बनाता है। θ का अधिकतम मान जब तक कि फुटबॉल तख्ते पर लोटना प्रारंभ नहीं करती है, इस तरह है कि [चित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है]
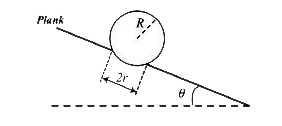
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
View Solutionनियत दाब पर एक आदर्श गैस की दी गई मात्रा के लिए निम्नलिखित में से कौन सा वक्र सही है?
View Solutionवायु के आधिक्य में सोडियम के दहन से एक उच्च ऑक्साइड प्राप्त होता है । उत्पाद में ऑक्सीजन की ऑक्सीकरण अवस्था क्या है ? ऋणात्मक चिन्ह की उपेक्षा कीजिए ।
View Solutionनिम्नलिखित में से कौन सा, 2s कक्षक के लिए इलेक्ट्रॉन के पाये जाने की अरीय प्रायिकता का सही मिलान है
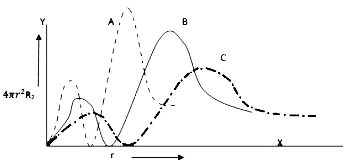
View Solutionएक एंजाइम उत्प्रेरित अभिक्रिया के लिए, ताप (T) के सापेक्ष अभिक्रिया की दर (r) को आलेखित किया गया है। निम्नलिखित में से कौन सा सही निरूपण है?
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solution298 K पर N_(2) गैस की जल में विलेयता के लिए हेनरी नियम का स्थिरांक 1xx10^(-5) atm है। वायु में N_(2) का मोल प्रभाज 0.8 है। यदि 298 K और 5 atm पर जल के 10 मोल में विलेय वायु के N_(2) के मोलों की संख्या x*10^(-4) है, तो x का मान ज्ञात कीजिए।
View Solutionनिम्नलिखित में से कौन सा विकल्प अभिक्रिया की स्वतः प्रवर्तिता के लिए सही है?
View Solutionध्रुवण का अर्थ होता है, "एक निकटतम स्थित धनायन द्वारा ऋणायन की आकृति में विकृति"। ध्रुवण के बारे में निम्नलिखित में से कौन सा कथन सही है?
View Solutionनिम्नलिखित में से कौन सी नाम अभिक्रिया एक -COOH समूह को निरूपित करने के लिए उपयोग नहीं की जाती है?
View Solution
