नीचे दी गयी सूची I में , एक कण के चार विभिन्न पथ , समय के विभिन्न फलनों के रूप में दिए गए है। इन फलनों में α और β उचित विमाओ वाले धनात्मक नियतांक है, जहाँ α≠βl प्रत्येक पथ में कण पर लगाने वाला बल या तो शून्य है या सरंक्षी है। सूची II में कण की पाँच भौतिक राशियों का विवरण दिया गया है p रेखीय संवेग है , L मूल बिन्दु के सापेक्ष कोणीय संवेग है K गतिज ऊर्जा है, U स्थितिज ऊर्जा है और E कुल ऊर्जा है। सूची I के प्रत्येक पथ का सूची II में दिए गए इन राशियों से समूएल कीजिए, जो उस पथ के लिए संरक्षी है।
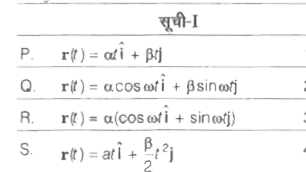
P→1,2,3,4,5, Q→2,5 ,R→2,3,4,5, S→5
P→1,2,3,4,5, Q→3,5 ,R→2,3,4,5, S→2,5
P→2,3,4, Q→5 ,R→1,2,4, S→2,5
P→1,2,3,5, Q→2,5 ,R→2,3,4,5, S→2,5
The correct Answer is:A
जब बल (F)=0⇒ स्थितिज ऊर्जा (U)− नियत
F≠0⇒ बल सरंक्षी ⇒ कुल ऊर्जा (E)= नियत
सूची I
(P)r(t)=αtˆi+βtˆj
drdt=V=αˆi+βˆj=नियतांक ⇒p= नियतांक
|V|=√α2+β2= नियतांक ⇒K= नियतांक
dVdt=a=0⇒F=0⇒U= नियतांक
E=U+K= नियतांक, L=m(r×v)=0
L= नियतांक
P→1,2,3,4,5
(Q)r(f)=αcosωtˆii+βcosωtˆj
drdt=V=aωsinωt(−ˆi)+βωcosωtˆj≠ नियतांक
⇒P≠ नियतांक
|V|=ω√(αsinωt)2+(βcosωt)2= नियतांक
K= नियतांक , a=dVdt=−ω2r≠0
⇒E= नियतांक =K+U
परन्तु , K= नियतांक ⇒U≠ नियतांक
L=m(r×v)=mωαβ(ˆk)= नियतांक
Q→2,5
(R)r(f)=α(cosωtˆi+sinωˆj)
drdt=V=αωsinωt(−ˆi)+cosωtˆj]≠ नियतांक
⇒P= नियतांक
|V|=αω=नियतांक ⇒K= नियतांक
a=dVdt=−ω2r≠0⇒E= नियतांक , U= नियतांक
L=m(r×v)=mωα2ˆk=नियतांक
R→2,3,4,5
(S)r(t)=αtˆi+β2t2ˆj
drdt=V=αˆi+βtˆj≠ नियतांक ⇒P≠नियतांक
|V|=√α2+(βt)2≠ नियतांक ⇒K≠ नियतांक
a=dVdt=βˆj≠0⇒E= नियतांक =K+U
परन्तु K≠ नियतांक
∴U≠ नियतांक
L=m(r×v)=12αβt2ˆk≠ नियतांक
S→5
Topper's Solved these Questions
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर 2-खण्ड 2
8 Videos
- सॉल्वड पेपर 2017 JEE MAIN संयुक्त प्रवेश परीक्षा BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर 2017 JEE MAIN संयुक्त प्रवेश परीक्षा EXERCISE - MCQs
30 Videos
- सॉल्वड पेपर्स 2020BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2020EXERCISE - PHYSICS
36 Videos
Similar Questions
एक ठोस क्षैतिज तल तेल के एक पतली परत से ढका हुआ है। द्रव्यमान m=0.4kg का एक आयताकार गुटका इस तल पर विरामावस्था में है। 1.0 न्यूटन से परिमाण का एक आवेग गुटके पर t=0 समय पर लगया जाता है जिसके फलस्वरूप गुटका x-अक्ष पर v(t)=v0e−t/τ वेग से चलने लगता है, जहाँ v0 एक स्थिर राशि है और τ=4 सेकण्ड है। समय t=τ पर गुटके का विस्थापन ................... मीटर है | e−1=0.37 ले
View Solutionएक प्रेक्षक प्रकाश गति की आधी गति से 10GHz आवृत्ति के एक स्थिर सूक्ष्म तरंग स्रोत की तरफ जा रहा है। प्रेक्षक द्वारा मापी गयी सूक्ष्म तरंग की आवृत्ति का मान होगा। (प्रकाश की चाल =3×108ms−1)
View Solutionक्षैतिज अवस्था में रखे हुए एक तख्ने (plank) में एक छिद्र है जिसकी त्रिज्या r है। तख्ते के इस छिद्र पर एक R(R>r) त्रिज्या वाले फुटबॉल को रखा गया है। जैसा कि नीचे चित्र में दिखाया गया है, इस तख्ते को अब एक छोर से ऊपर उठाया जाता है जिससे कि यह उन्नत हो कर क्षितिज से θ का कोण बनाता है। θ का अधिकतम मान जब तक कि फुटबॉल तख्ते पर लोटना प्रारंभ नहीं करती है, इस तरह है कि [चित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है]
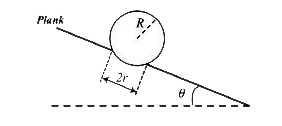
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionनिम्नलिखित गद्यांश को ध्यानपूर्वक पढ़कर पूछे गए प्रश्नों के उत्तर लिखिए:
अकसर हम या तो गुजरे हुए दिनों की खट्टी-मीठी यादों में उलझे रहते हैं या भविष्य के रंगीन सपने देखते हैं। हम या तो भूतकाल में रहते हैं या भविष्यकाल । असल में दोनों काल मिथ्या हैं। एक चला गया है, दूसरा आया नहीं है। हमारे सामने जो वर्तमान क्षण है, वही सत्य है। उसी में जीना चाहिए।
गद्यांश में लेखक ने किन बातों में उलझे रहने की बात कही है?
View Solutionपत्रकारिता के विभिन्न आयामों में से एक है
View Solutionराजस्थान में वर्षा की मात्रा नापने में इंच या सेंटीमीटर के स्थान पर किस शब्द का प्रयोग होता है ?
View Solutionपत्रकारिता के विभिन्न आयामों में से एक है
View Solutionहामिद के चरित्र की विभिन्न विशेषताओं में से एक विशेषता है
View Solutionविरंजक चूर्ण में इसके एक घटक के रूप में एक ऑक्सोअम्ल का लवण होता है। इस अम्ल का एनहाइड्राइड है:
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionनिम्नलिखित में से कौनसा दिए गए यौगिकों में सक्रियता के सही क्रम का निरूपण करता है?
View Solutionनीचे दिए गए चार तत्वों पर विचार कीजिए, जिन्हें आवर्त सारणी के दीर्घाकार रूप के अनुसार निरूपित किया गया है,
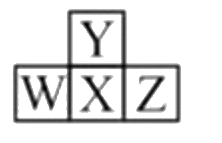
यहाँ W, Y और Z तत्व 'X' के संदर्भ में बाएं, ऊपर और दाएं उपस्थित हैं और तत्व 'X' सोलहवें वर्ग और तीसरे आवर्त से संबंधित हैं। तब दी गई सूचना के अनुसार दिए गए तत्वों के बारे में गलत कथन है :
View Solutionब्यूटेन-2, 3-डाइऑल के विभिन्न संरूपणों की संख्या के संबंध में निम्नलिखित में से कौनसा कथन सत्य है?
View Solutionविभिन्न कार्बनिक अभिक्रियाओं में BF_3 का उपयोग उत्प्रेरक के रूप में किया जाता है क्योंकि:
View Solution
