चित्रानुसार तीन काँच के बेलन , जिनकी ऊँचाई H = 30 सेमी तथा अपवर्तनांक n = 1.5 है , को एक क्षैतिज सतह पर रखा गया है । बेलन- I की ऊपरी सतह समतल , बेलन- II की ऊपरी सतह उत्तल तथा बेलन- III की ऊपरी सतह अवतल है । दोनों वक्रीय सतहों की वक्रता त्रिज्या समान तथा R = 3 मी है । यदि तीनों बेलनों के नीचे उपस्थित एक बिन्दु x की आभासी गहराइयाँ H1,H2 और H3 हैं , तो निम्नलिखित कथनों में से कौन - सा ( से ) सही है / हैं ) ?
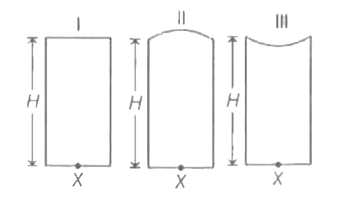
H2>H1
H3>H1
0.8cm<H2&H1<0.9cm
H2>H3
The correct Answer is:A, D
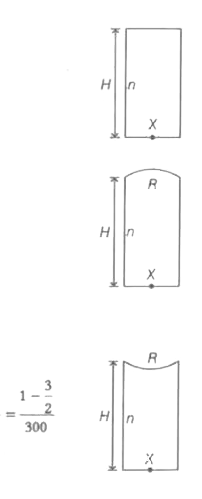
(a,d) स्थिति-I
H=30cm
n=32
H1=Hn⇒30×23=20cm
स्थिति-II
R=300cm
n2v−n1u=n2−n1R
1−H2−3(−2×30)=1−32−300
⇒H2=60029=20.684cm
स्थिति-III
n2v−n1u=n2−n1R,1−H3−3(−2×30)=1−32300
⇒H3=60031=19.354cm
Topper's Solved these Questions
- JEE ADVANCED सॉल्वड पेपर -2019BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सॉल्वड पेपर -2019EXERCISE - पेपर 2- खण्ड 2
6 Videos
- JEE ADVANCED सॉल्वड पेपर -2019BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सॉल्वड पेपर -2019EXERCISE - पेपर 2- खण्ड 3
4 Videos
- JEE ADVANCED सॉल्वड पेपर -2019BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सॉल्वड पेपर -2019EXERCISE - पेपर 1 - खण्ड 3
6 Videos
- JEE ADVANCED पेपर - 1 (2012)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 1 (2012)EXERCISE - भाग -I भौतिक विज्ञान खंड - III : पूर्णांक उत्तर प्रकार
5 Videos
Similar Questions
माना कि एक स्थिर 22688Ra नाभिक अपनी निम्नतम अवस्था ( Ground state ) α -क्षय करके एक उत्तेजित अवस्था वाले ( Excited state ) 22286Rn नाभिक में क्षयित होता है । उत्सर्जित होने वाले -कण की गतिज ऊर्जा 4.44 Mev है । 22286Rn नाभिक फिर Y- क्षय करके अपनी निम्नतम अवस्था में आता है । उत्सर्जित Y फोटॉन की ऊर्जा...... keV दिया है
, 22688Ra का परमाण्विक द्रव्यमान ( Atomic mass ) = 226.005 u , 22286Rn का परमाण्विक द्रव्यमान = 222.000 u , α कण का परमाण्विक द्रव्यमान = 4.000 u , 1 u = 931 MeVc2 , c प्रकाश की गति है .
View Solutionएक वाद्य - यन्त्र को चार भिन्न धातु की तारों 1 , 2 , 3 और 4 से बनाया गया है , जिनके एकांक लम्बाई के द्रव्यमान ( Mass per unit length ) क्रमशः μ, 2μ, 3μ तथा 4μ हैं । इस यन्त्र के तारों को मुक्त लम्बाई L0 से 2L0 के बीच परिवर्तित करते हुए कंपित करके बजाया जाता है । पाया जाता है कि तार 1(μ) की मुक्त लम्बाई L0 , पर तनाव T0के कारण मूल विधा की आवृत्तिf0 है ।
सूची- I में ऊपर दी गयी चार तारें हैं । सूची- II में किसी मात्रा का परिमाण है ।

तार 1 , 2 , 3 और 4 की लम्बाइयों का मान क्रमशः L0,3L02,5L04और7L04 है । तार 1 , 2 , 3 और 4 को क्रमशः उनकी प्रथम ( 1st ) , तृतीय ( 3rd ) , पंचम ( 5th ) तथा चौदहवीं ( 14th ) गुणावृत्तियों पर इस तरह से कंपित करते हैं कि सभी तारों की आवृत्तियाँ समान रहती हैं । चारों तारों के तनाव का T0 इकाई में सही मिलान हो
View Solutionएक धारिता C वाले समान्तर प्लेट स्धारित्र के प्लेटो के बीच कि दूरी d है और प्रत्यक प्लेट का क्षेत्रफल A है| प्लेटो के बीच का पूरा स्थान प्लेटो के समान्तरδ=dN मोटाई वाली N प्रवेघुत परतो से भरा है| m वें परत का प्रवेघुतांकKm=K(1+mN) है| बहुत अधिक N(>103) के लिए धारिताC=α(Kε0Adln2) है| α का मान............होगा
[मुक्त आकाश (Free space) की वेघुतशीलता ε0 है]
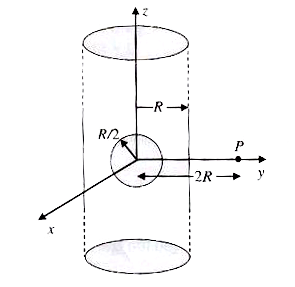
View Solutionअपरिमित लम्बाई और R त्रिज्या के एक ठोस बेलन पर एकसमान आयतन-आवेश-घनत्व ρ है। इसमें R/2 त्रिज्या का
एक खोखला गोलीय-कोष बेलन के अक्ष पर केन्द्रित है (चित्र देखिये)। अक्ष से 2R दूरी पर स्थित बिन्दु P पर वैद्युत-क्षेत्र
23ρR16kε0 से दिया जाता है । तब k का मान क्या है?
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solutionमुक्त शरीर आरेख | समतल सतह पर वस्तु की गति -1
View Solutionसमतल सतह पर वस्तु की गति -2
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionसमतल घर्षण वाले सतह पर वस्तु की गति
View Solutionसमतल घर्षण वाले सतह पर वस्तु की गति -2
View Solutionमुक्त शरीर आरेख | समतल सतह पर वस्तु की गति -1
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View SolutionA cube is placed inside a cone of radius 20cm and height 10cm, one of its face being on the base of the cone and vertices of opposite face touching the cone. What is the length (in cm) of side of the cube? एक घन को एक शंकु जिसकी त्रिज्या 20 से. मी. तथा ऊँचाई 10 से.मी. है, के अंदर रखा जाता है, उसको एक सतह शंकु के आधार कौर ओर है तथा विपरीत सतह के शीर्ष शंकु का स्पर्श कर रहे है। घन की भुजा लम्बाई (से. मी. में) क्या है ?
View SolutionA cylinder of radius 4.5 cm and height 12 cm just fits in another cylinder completely with their axis perpendicular. What is the radius (in cm) of second cylinder? एक बेलन जिसकी त्रिज्या 4.5 से.मी. तथा ऊँचाई 12 से.मी. है, को एक अन्य बेलन में उनके अक्षों के लम्बवत् पूरी तरह से सम्माहित किया गया है। दूसरे बेलन की त्रिज्या (से.मी. में) क्या है?
View SolutionA hollow cylinder of thickness 0.7 cm and height 15cm is made of iron. If inner radius of cylinder is 3.5 cm, then what is the total surface area (in cm^2 ) of the hollow cylinder? एक लोहे से बने बेलन की चौड़ाई 0.7 सेमी. तथा ऊँचाई 15 सेमी. है। यदि बेलन की आंतरिक त्रिज्या 3.5 सेमी. है, वो खाली बेलन का कुल पृष्ठीय क्षेत्रफल ( सेमी^2 में) क्या है?
View Solution
