A body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
32
96
34
80
The correct Answer is:B
To find the percentage change in kinetic energy of the first body after an elastic collision, we can follow these steps:
Step 1: Determine the initial kinetic energy of the first body.
The initial kinetic energy (KE_initial) of the first body (mass = m/2, velocity = v_0) is given by the formula:
KEinitial=12(m2)v20=mv204
Step 2: Apply conservation of momentum.
In an elastic collision, both momentum and kinetic energy are conserved. The initial momentum of the system is:
pinitial=(m2)v0+0=mv02
Let v1 be the final velocity of the first body and v2 be the final velocity of the second body (mass = m/3). The final momentum is:
pfinal=(m2)v1+(m3)v2
Setting the initial momentum equal to the final momentum:
mv02=(m2)v1+(m3)v2
Dividing through by m:
v02=12v1+13v2
Step 3: Apply conservation of kinetic energy.
The initial kinetic energy is equal to the final kinetic energy:
KEinitial=KEfinal
mv204=12(m2)v21+12(m3)v22
Dividing through by m:
v204=14v21+16v22
Step 4: Solve the equations.
From the momentum equation:
v02=12v1+13v2
Multiply through by 6 to eliminate fractions:
3v0=3v1+2v2(1)
From the kinetic energy equation:
v204=14v21+16v22
Multiply through by 12:
3v20=3v21+2v22(2)
Step 5: Substitute and solve for v1 and v2.
From equation (1):
2v2=3v0−3v1⇒v2=3v0−3v12
Substituting v2 into equation (2):
3v20=3v21+2(3v0−3v12)2
Expanding and simplifying will yield values for v1 and v2.
Step 6: Calculate the final kinetic energy of the first body.
Once we find v1, we can calculate the final kinetic energy:
KEfinal=12(m2)v21
Step 7: Calculate the percentage change in kinetic energy.
The percentage change in kinetic energy is given by:
Percentage Change=KEinitial−KEfinalKEinitial×100
Final Calculation:
Substituting the values of KEinitial and KEfinal into the percentage change formula will yield the final result.
The initial kinetic energy (KE_initial) of the first body (mass = m/2, velocity = v_0) is given by the formula:
KEinitial=12(m2)v20=mv204
In an elastic collision, both momentum and kinetic energy are conserved. The initial momentum of the system is:
pinitial=(m2)v0+0=mv02
Let v1 be the final velocity of the first body and v2 be the final velocity of the second body (mass = m/3). The final momentum is:
pfinal=(m2)v1+(m3)v2
Setting the initial momentum equal to the final momentum:
mv02=(m2)v1+(m3)v2
Dividing through by m:
v02=12v1+13v2
The initial kinetic energy is equal to the final kinetic energy:
KEinitial=KEfinal
mv204=12(m2)v21+12(m3)v22
Dividing through by m:
v204=14v21+16v22
From the momentum equation:
v02=12v1+13v2
Multiply through by 6 to eliminate fractions:
3v0=3v1+2v2(1)
v204=14v21+16v22
Multiply through by 12:
3v20=3v21+2v22(2)
From equation (1):
2v2=3v0−3v1⇒v2=3v0−3v12
Substituting v2 into equation (2):
3v20=3v21+2(3v0−3v12)2
Expanding and simplifying will yield values for v1 and v2.
Once we find v1, we can calculate the final kinetic energy:
KEfinal=12(m2)v21
The percentage change in kinetic energy is given by:
Percentage Change=KEinitial−KEfinalKEinitial×100
Substituting the values of KEinitial and KEfinal into the percentage change formula will yield the final result.
Topper's Solved these Questions
Similar Questions
A body of mass m moving with velocity v collides head-on elastically with another body of mass 2m which is initially at rest. The ratio of K. E. of mass m before and after the collision will be
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View Solution
Knowledge Check
A body of mass m moving with velocity uˆi collides elastically with a body at rest of mass 3m and then the final velocity of body mass m is v ˆj. Find the relation between v and u
Au = 2vBu = v/2Cu = _√2 vDu = v/_√2A ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
A−v,2vB−2v,vCv,−2vD2v,−vA body of mass M moves with velocity v and collides elasticity with another body of mass m(M>>m) at rest , then the velocity of the body of mass m is
AvB2vCv/2DZero
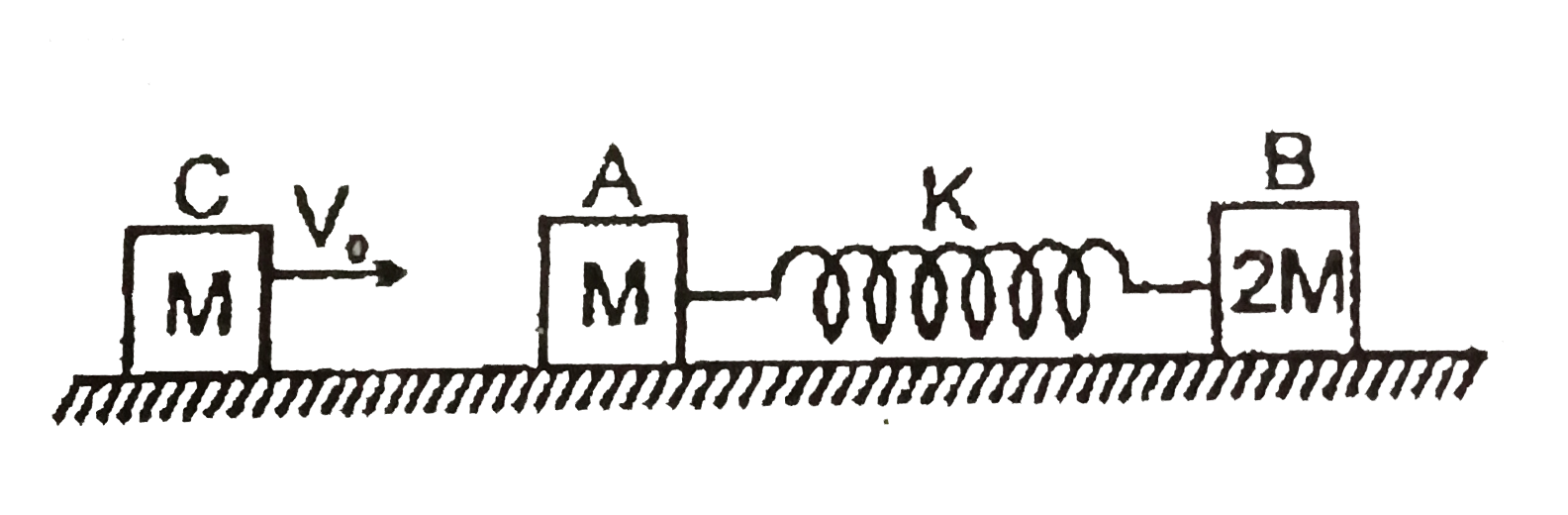 Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same
Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same
View SolutionA body of mass M moves with velocity v and collides elasticity with another body of mass m(M>>m) at rest , then the velocity of the body of mass m is
View SolutionA block C of mass m is moving with velocity v0 and collides elastically with block A of mass m and connect to another block B of mass 2m through spring constant k. What is k if x0 is compression of spring when velocity of A and B is same ?
View SolutionA block C of mass m is moving with velocity v0 and collides elastically with block A of mass m and connect to another block B of mass 2m through spring constant k. What is k if x0 is compression of spring when velocity of A and B is same ?

View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View Solution
