In flask two components A & B are mixed in which both concentrations are equal . Half life of A is 300s & B is 180s. It is first order kinetics & find at what time concentration A becomes 4 times of concentration of B.
900s
300s
120s
180s
To solve the problem step by step, let's break down the information provided and apply the first-order kinetics equations.
Step 1: Understand the Given Information
- We have two components A and B mixed in equal concentrations initially.
- The half-life of A (t_half_A) = 300 seconds.
- The half-life of B (t_half_B) = 180 seconds.
- We need to find the time (t) when the concentration of A (C_A) becomes 4 times the concentration of B (C_B).
Step 2: Calculate the Rate Constants (k)
For first-order kinetics, the rate constant (k) can be calculated using the formula:
k=ln(2)t1/2
Calculating k for A:
kA=ln(2)300
Calculating k for B:
kB=ln(2)180
Step 3: Write the Concentration Equations
For first-order reactions, the concentration at time t can be expressed as:
Ct=C0e−kt
For component A:
CA(t)=C0e−kAt
For component B:
CB(t)=C0e−kBt
Step 4: Set Up the Equation for the Given Condition
We want to find the time when:
CA(t)=4CB(t)
Substituting the expressions for CA(t) and CB(t):
C0e−kAt=4(C0e−kBt)
Dividing both sides by C0:
e−kAt=4e−kBt
Step 5: Rearranging the Equation
Rearranging gives:
e−kAte−kBt=4
e−(kA−kB)t=4
Taking the natural logarithm of both sides:
−(kA−kB)t=ln(4)
Step 6: Substitute the Values of k_A and k_B
Substituting the values of k_A and k_B:
kA−kB=ln(2)300−ln(2)180
Finding a common denominator (which is 900):
kA−kB=3ln(2)900−5ln(2)900=−2ln(2)900
Step 7: Substitute Back into the Equation
Now substituting back into our equation:
−(−2ln(2)900)t=ln(4)
Since ln(4)=2ln(2):
2ln(2)900t=2ln(2)
Step 8: Solve for t
Cancelling 2ln(2) from both sides:
1900t=1
t=900 seconds
Final Answer
The time at which the concentration of A becomes 4 times that of B is 900 seconds.
---
- We have two components A and B mixed in equal concentrations initially.
- The half-life of A (t_half_A) = 300 seconds.
- The half-life of B (t_half_B) = 180 seconds.
- We need to find the time (t) when the concentration of A (C_A) becomes 4 times the concentration of B (C_B).
For first-order kinetics, the rate constant (k) can be calculated using the formula:
k=ln(2)t1/2
kA=ln(2)300
kB=ln(2)180
For first-order reactions, the concentration at time t can be expressed as:
Ct=C0e−kt
CA(t)=C0e−kAt
CB(t)=C0e−kBt
We want to find the time when:
CA(t)=4CB(t)
C0e−kAt=4(C0e−kBt)
e−kAt=4e−kBt
Rearranging gives:
e−kAte−kBt=4
e−(kA−kB)t=4
−(kA−kB)t=ln(4)
Substituting the values of k_A and k_B:
kA−kB=ln(2)300−ln(2)180
kA−kB=3ln(2)900−5ln(2)900=−2ln(2)900
Now substituting back into our equation:
−(−2ln(2)900)t=ln(4)
2ln(2)900t=2ln(2)
Cancelling 2ln(2) from both sides:
1900t=1
t=900 seconds
The time at which the concentration of A becomes 4 times that of B is 900 seconds.
Similar Questions
Knowledge Check
For a first order reaction, if ‘a’ is the initial concentration of reactant, then the half life time is
Aindependent of aB∝aC∝a2D∝a3Half life of a first order reaction is 4s and the initial concentration of the reactant is 0.12 M. The concentration of the reactant left after 16 s is
A0.0075 MB0.06MC0.03 MD0.015M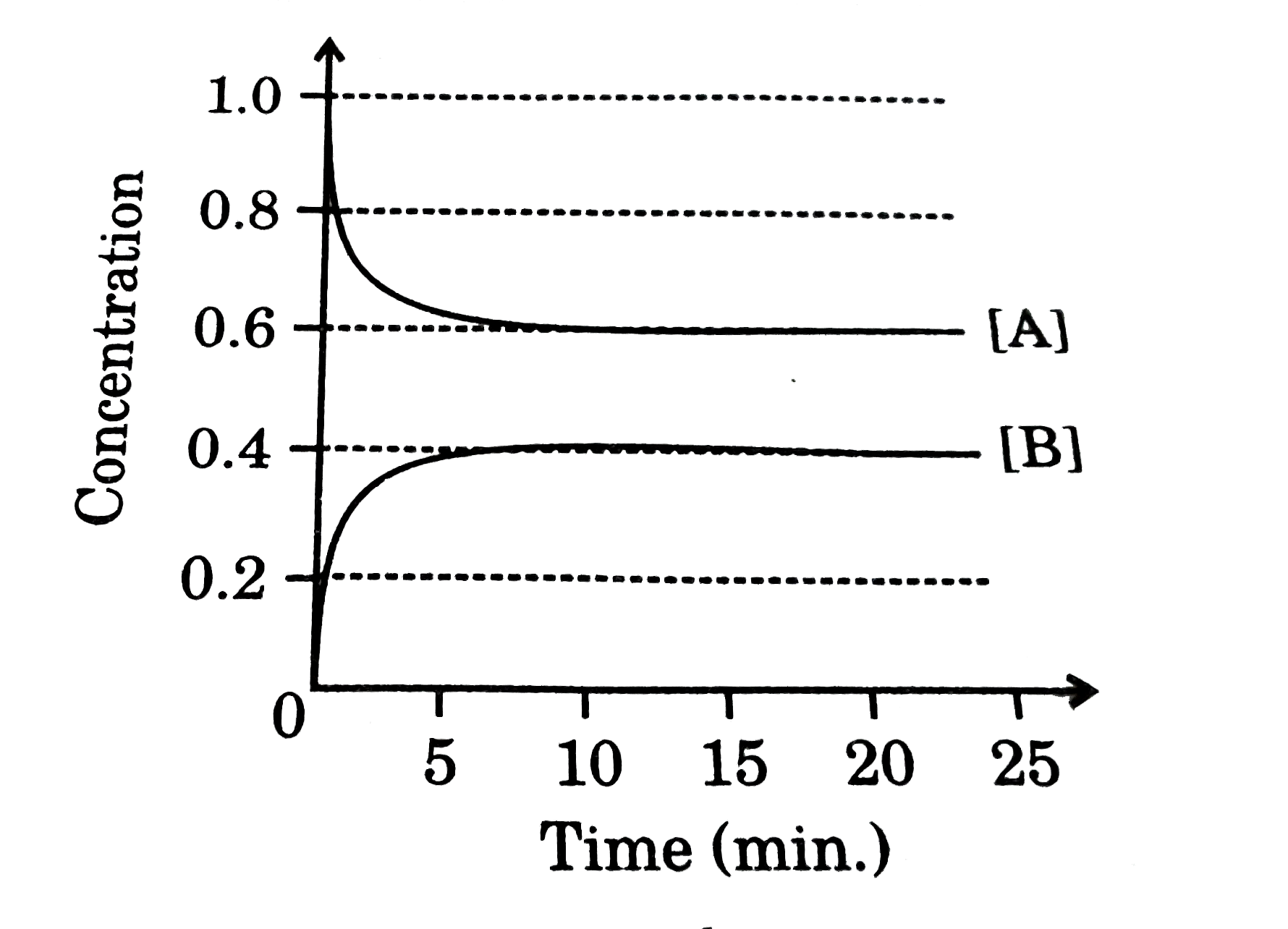
For the reversible reaction Akf⇐===⇒kbB (having Ist order in both direction) the concentration as a function of time are given for a certain experimantal run.
At what time (t) is the rete of change of concentration A equal to the rate of change of concentration of B in magnitude?At=0onlyBt≥tequilibriumonlyCt=0min onlyDAt all times
For a first order reactions, the half -life is 10 mins. How much time in minutes will it take to reduce the concentration of reactant to 25% of its original concentration ?
View SolutionFor the first order reaction half-life time is ………….. on the initial concentration.
View SolutionA flask contains a mixture of two compounds AB and XY. Both of these decompose on heating by first order reaction. If the half-life of AB is 30 min and that of XY is 10 min, how long will it take for the concentration of AB to be four times that of XY ? Assume that the initial concentration of both AB and XY to be same.
View SolutionThe reaction A+B→ products is first order in each of the reactants.
(a) How does the rate of reaction change if the concentration of A is increased by factor 3 ?
(b) What is the change in the rate of reaction if the concentration of A is halved and concentration of B is doubled ?
View SolutionThe half life period of a first order reaction, A → Product is 10 minutes. In how much time is the concentration of A reduced to 10% of its original concentration?
View Solution
