A body at a temperature of 500F is placed outdoors where the temperature is 1000F . If the rate of change of the temperature of a body is proportional to the temperature difference between the body and its surrounding medium. If after 5 min the temperature of the body is 600F , find (a) how long it will take the body to reach a temperature of 75 ^0 F and (b) the temperature of the body after 20 min.
To solve the problem, we will use Newton's Law of Cooling, which states that the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature.
1. Set Up the Equation:
Let T be the temperature of the body at time t, and let Tm=100∘F be the surrounding temperature. According to Newton's Law of Cooling, we can write:
dTdt=k(Tm−T)
where k is a positive constant of proportionality.
2. Substituting Known Values:
We know that initially, the temperature of the body is T(0)=50∘F. After 5 minutes, the temperature is T(5)=60∘F.
3. Integrate the Differential Equation:
Rearranging the equation gives:
dTTm−T=kdt
Integrating both sides:
−ln|Tm−T|=kt+C
Exponentiating gives:
Tm−T=Ce−kt
where C is a constant.
4. Finding the Constant C:
At t=0:
Tm−T(0)=100−50=50⟹C=50
Thus, the equation becomes:
Tm−T=50e−kt
or
T=100−50e−kt
5. Using the Condition at t=5:
Substitute t=5 and T(5)=60:
60=100−50e−5k
Rearranging gives:
50e−5k=40⟹e−5k=45
Taking the natural logarithm:
−5k=ln(45)⟹k=−15ln(45)
6. Finding Time to Reach 75∘F:
Set T=75:
75=100−50e−kt
Rearranging gives:
50e−kt=25⟹e−kt=12
Taking the natural logarithm:
−kt=ln(12)⟹t=−ln(12)k
Substitute k:
t=−ln(12)−15ln(45)=5ln(2)ln(45)
Calculate t using logarithmic values.
7. Finding the Temperature After 20 Minutes:
Substitute t=20:
T(20)=100−50e−20k
Substitute k and calculate T(20).
Let T be the temperature of the body at time t, and let Tm=100∘F be the surrounding temperature. According to Newton's Law of Cooling, we can write:
dTdt=k(Tm−T)
where k is a positive constant of proportionality.
We know that initially, the temperature of the body is T(0)=50∘F. After 5 minutes, the temperature is T(5)=60∘F.
Rearranging the equation gives:
dTTm−T=kdt
Integrating both sides:
−ln|Tm−T|=kt+C
Exponentiating gives:
Tm−T=Ce−kt
where C is a constant.
At t=0:
Tm−T(0)=100−50=50⟹C=50
Thus, the equation becomes:
Tm−T=50e−kt
or
T=100−50e−kt
Substitute t=5 and T(5)=60:
60=100−50e−5k
Rearranging gives:
50e−5k=40⟹e−5k=45
Taking the natural logarithm:
−5k=ln(45)⟹k=−15ln(45)
Set T=75:
75=100−50e−kt
Rearranging gives:
50e−kt=25⟹e−kt=12
Taking the natural logarithm:
−kt=ln(12)⟹t=−ln(12)k
Substitute k:
t=−ln(12)−15ln(45)=5ln(2)ln(45)
Calculate t using logarithmic values.
Substitute t=20:
T(20)=100−50e−20k
Substitute k and calculate T(20).
Similar Questions
Knowledge Check
For a small temperature difference between the body and the surroundings, the relation between the rate of heat loss R and the temperature of the body is depicted by
A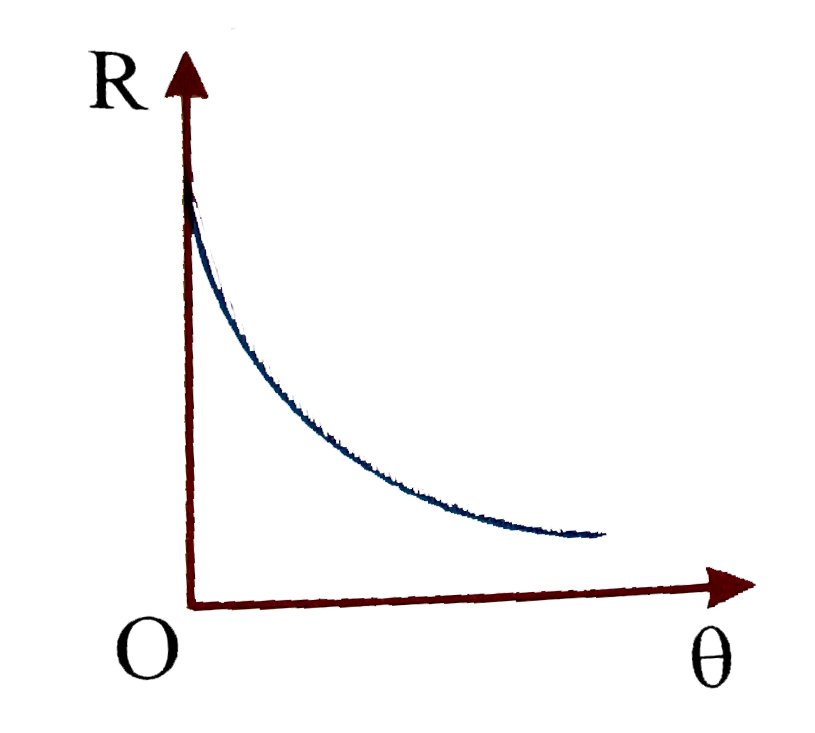 B
B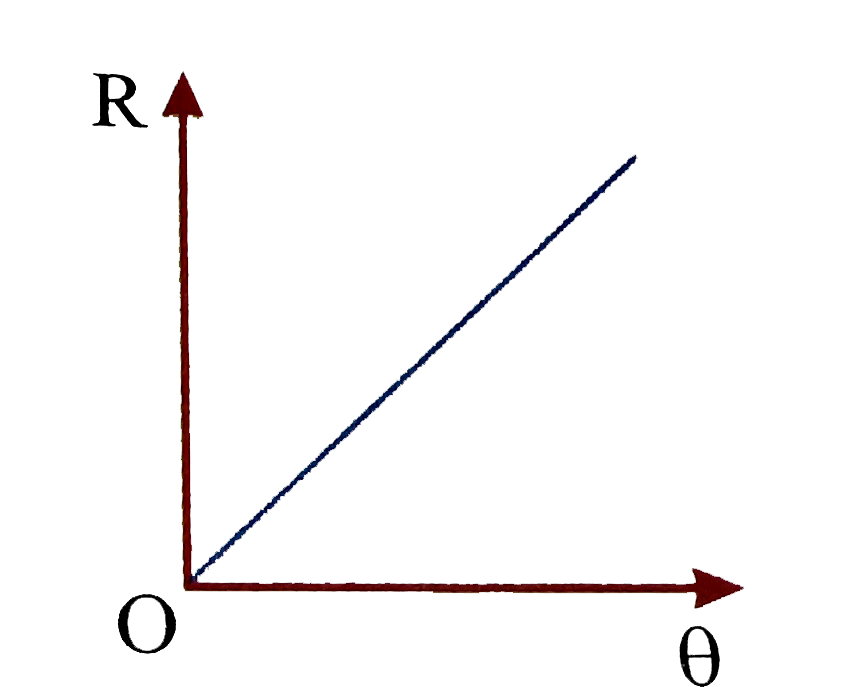 C
C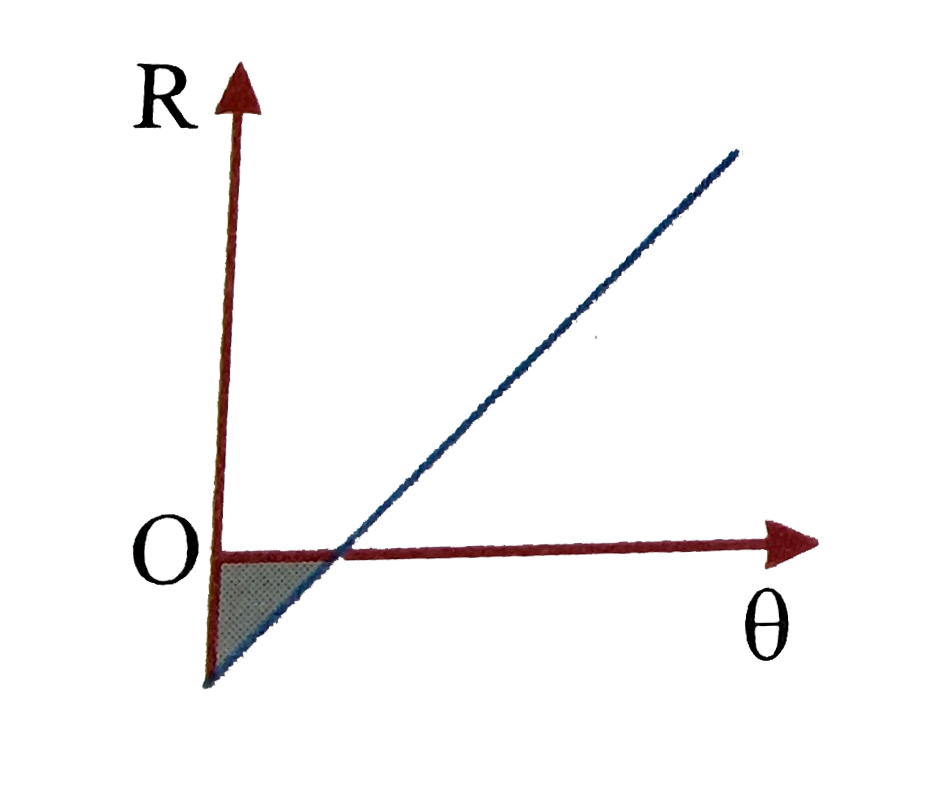 D
D
For a small temperature difference between the body and the surroundings the relation between the rate of loss heat R and the temperature of the body is depicted by
A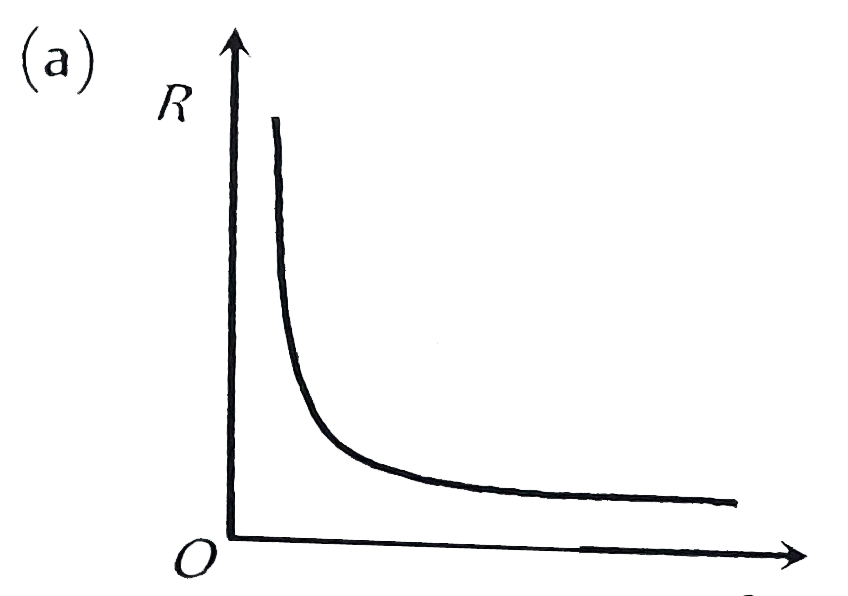 B
B C
C D
D
The change in temperature of a body is 20∘C, then the change in temperature of Kelvin scale is :-
A293 KB25 KC20 KD253 K
Change in temperature of a body is 57∘C . The equivalent change in temperature in kelvin scale is ________.
View SolutionBody A has the temperature 100∘F and body B has temperature 100 K. If they are brought in contact, then
View SolutionAs difference of temperature of body and surroundings increases, rate of cooling
View SolutionThe change in temperature of a body is 20∘C, then the change in temperature of Kelvin scale is :-
View SolutionWhen a body has the same temperature as that of its surroundings
View Solution
