Find distance of centre of mass of solid hemisphere of radius 8cm from centre
3 cm
3/8 cm
4 cm
2 cm
The correct Answer is:A
To find the distance of the center of mass of a solid hemisphere from its center, we can follow these steps:
1. Understand the Geometry:
- We have a solid hemisphere with a radius r. The center of the flat circular base of the hemisphere is at point O, and the center of mass C is located along the vertical axis from O to the flat face.
2. Identify the Formula for Center of Mass:
- For a solid hemisphere, the distance of the center of mass from the flat face (the base) is given by the formula:
h=3r8
- Here, h is the distance from the flat surface to the center of mass, and r is the radius of the hemisphere.
3. Substitute the Given Radius:
- The radius of the hemisphere is given as r=8cm.
- Substituting this value into the formula:
h=3×88
4. Simplify the Expression:
- Simplifying the expression:
h=248=3cm
5. Conclusion:
- Therefore, the distance of the center of mass C from the center O of the hemisphere is 3cm.
Final Answer:
The distance of the center of mass of the solid hemisphere from the center is 3 cm.
---
- We have a solid hemisphere with a radius r. The center of the flat circular base of the hemisphere is at point O, and the center of mass C is located along the vertical axis from O to the flat face.
- For a solid hemisphere, the distance of the center of mass from the flat face (the base) is given by the formula:
h=3r8
- Here, h is the distance from the flat surface to the center of mass, and r is the radius of the hemisphere.
- The radius of the hemisphere is given as r=8cm.
- Substituting this value into the formula:
h=3×88
- Simplifying the expression:
h=248=3cm
- Therefore, the distance of the center of mass C from the center O of the hemisphere is 3cm.
The distance of the center of mass of the solid hemisphere from the center is 3 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3 - Question 2 - Select One
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A335cmB135cmC310cmDNone of these
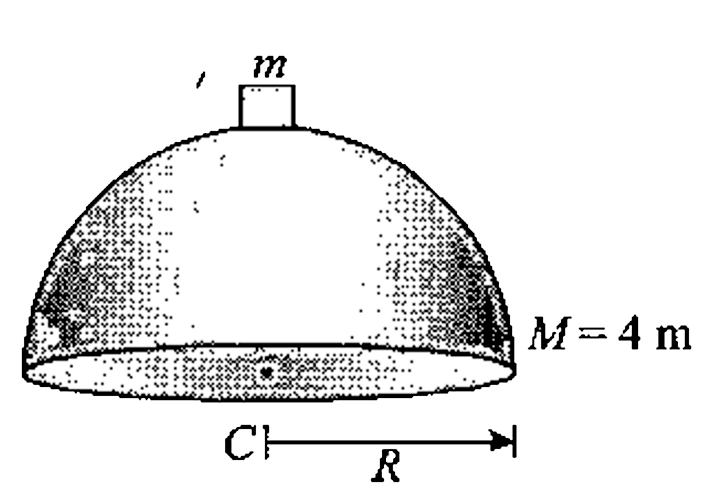
A small block of mass m starts sliding down from rest along the smooth surface of a fixed hollow hemisphere of same mass m. Find the distance of centre of mass of block and hemishere from centre of hemisphere C when block m separates from the surface of hemisphere.
 View Solution
View SolutionThe centre of gravity of a solid hemisphere of radius a is : (A)
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionWhat can be said about the centre of mass of a solid hemisphere of radius r without making any calculation. Will its distance from the centre be more than r/2 or less than r/2?
View SolutionLocate the position of the centre of mass of a hemisphere of radius R as shown in the following figure:
 View Solution
View SolutionDetermine the position of the centre of mass of a hemisphere of radius R.
View Solution

