the area of region for which 0<y<3−2x−x2 and x>0 is
Step by step video & image solution for the area of region for which 0 lt y lt 3 - 2x-x^2 and x gt 0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Let L=4x−5y,Li=x10−in,Li=x10+y8+in, and E=x250+y232−1. LetAi repersents the area of region common between Li−1>0,Li<0,E<0 and L<0, A'i represents the area of region common between L'i−1<0,L'i>0,E<0 and L<0. Bi repersents the area of region common between Li−1>0,Li<0,E<0 and L>0, B'i repersents the area of region common between L'i−1<,L'i>0,E<0 and L>0, then value of (A1+A'2+A3+A'4+.......)+(B1+B'2+B'4+.......) is equal to .
View SolutionWhich of the folowing should be the feasible region of the system of linear lnequalities x + 2y ≤12,2x+y≤12,4x+5y≥20 and x,y≥0 ?
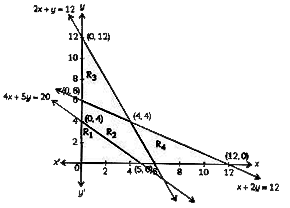
View Solution
Knowledge Check
The area of the region for which o<y<3−2x−x2 and x>0, is
A3∫1(3−2x−x2)dxB3∫0(3−2x−x2)dxC1∫0(3−2x−x2)dxD3∫−1(3−2x−x2)dxA polynomial P is positive for x<0, and the area of the region bounded by P(x), then x-axis, and the vertical lines x=0andx=K is K2(K+3)/3. The polynomial P(x) is
Ax2+2xBx2+x+1Cx2+2x+1Dx3+1What is the area of the region bounded by |x|<5.y=0 and y=8?
A40 sq unitB80 sq.unitC120 sq. unitD160 sq. unit
Area of the region bounded by the curve y={x2x<0xx≥0 and the line y=4 is (A) 103 (B) 203 (C) 503 (D) none of these
View SolutionSuppose y=f(x) and y=g(x) are two continuous functiond whose graphs intersect at the three points (0,4),(2,2) and (4,0) with f(x)>g(x) for 0<x<2 and f(x)<g(x) for 2<x<4. If ∫40[f(x)−g(x)]dx=10and∫42[g(x)−f(x)]dx=5 the area between two curves for 0<x<2,is (A) 5 (B) 10 (C) 15 (D) 20
View SolutionWhich of the following is a corner point of the feasible region of system of linear inequations 2x + 3y ≤6,x+4y≤4 and x, y ≥0 ?
View SolutionLet S is the region of points which satisfies y2<16x,x<4andxy(x2−3x+2)x2−7x+12>0. Its area is
View SolutionIf x<0<y, then :
View Solution
