If AB and CD are perpendicular diameters of circle Q. and ∠QPC=60∘, then the length of PQ divided by, the length of AQ is:-
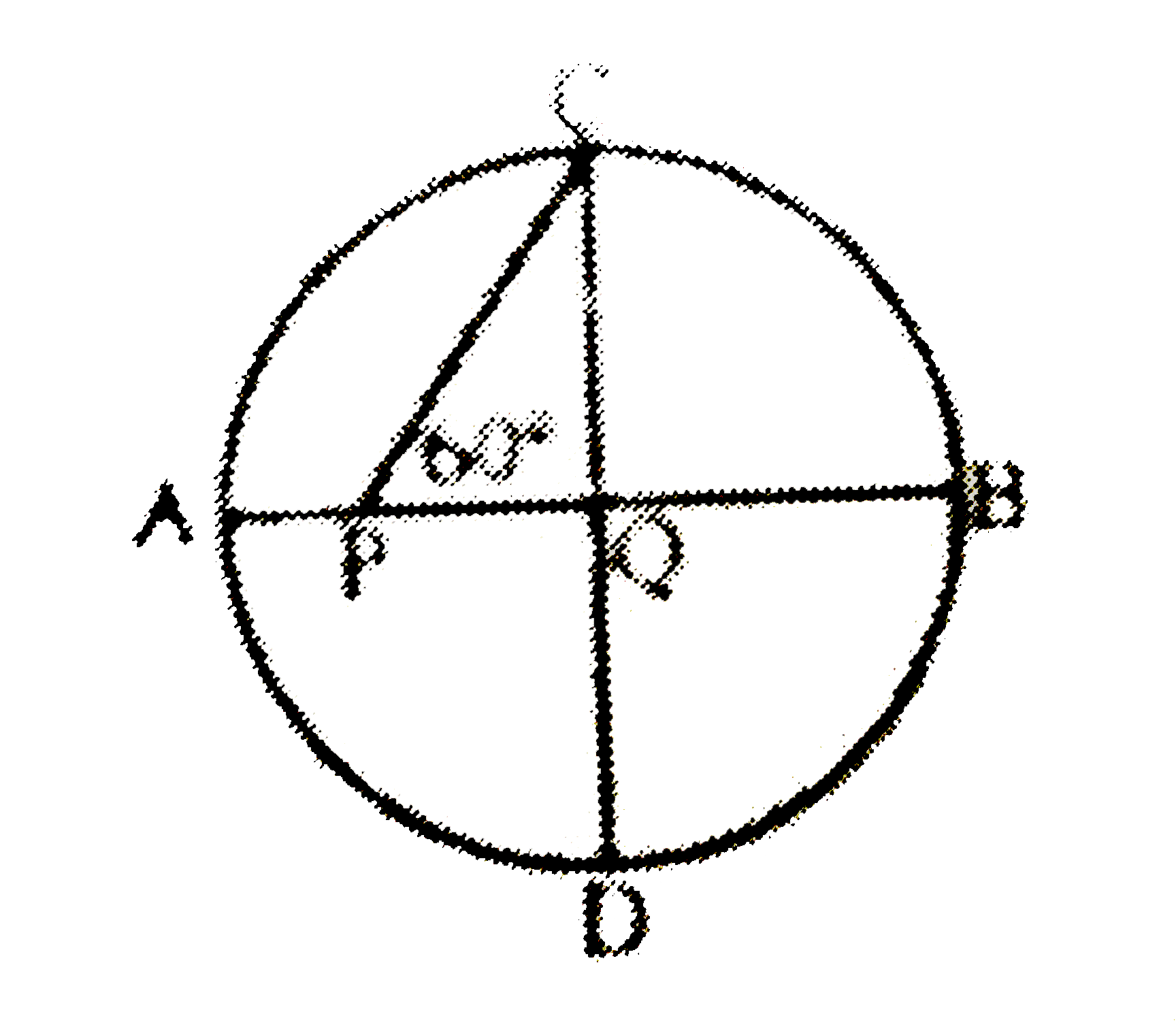
√32
√33
√22
12
The correct Answer is:B
Step by step video, text & image solution for If AB and CD are perpendicular diameters of circle Q. and /_QPC = 60^(@), then the length of PQ divided by, the length of AQ is:- by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 4
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 5
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 2
10 Videos
- LOGARITHMSBOOK - ALLENCHAPTER - LOGARITHMSEXERCISE - All Questions
107 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
12 Videos
Similar Questions
Knowledge Check
ABC is a triangle inscribed in a circle, AC being the diameter of the circle. The length of AC is as much more than the length of BC as the length of BC is more than the length of AB. Find AC:AB.
A5:3B5:4C6:5D3:2Chord PQ is the perpendicular bisector of radius OA of circle with centre O (A is a point on the edge of the circle). If the length of Arc PAQ=2π3 . What is the length of chord PQ?
A2B√3C2√3D1In a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
A1. 36∘B2. 24∘C3. 48∘D4. 12∘
In the given figure, AB || DE. Find the length of CD.
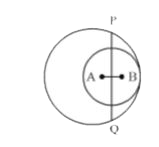
View SolutionTwo circles whose centres are A & B touches internally to each other as shown in figure their radii are 5 and 3 units respectively. The perpendicular bisector of AB meets at P and Q on the outer circle. Find the length of PQ.
View SolutionAB and CD are two diameters of a circle of radius r and they are mutually perpendicular. What is the ratio of the area of the circle to the area of the triangle ACD?
View SolutionAB and CD are two parallel chords of a circle such that AB = 6 cm and CD = 2AB. Both chords are on the same side of the centre of the circle. If the distance between is equal to one-fourth of the length of CD, then the radius of the circle is-
AB और CD किसी वृत्त की दो ऐसी समानांतर जीवाएं है कि AB = 6 सेमी है और CD = 2AB है | दोनों जीवाएं वृत्त के केंद्र के एक ही तरफ हैं | यदि बीच की दूरी CD की लंबाई के एक चौथाई के बराबर है, तो वृत्त की त्रिज्या ज्ञात करें |
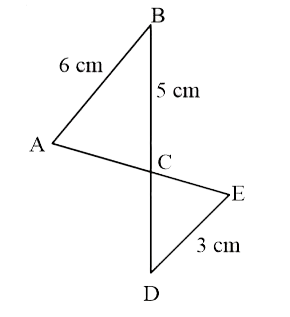
View SolutionChords AB and CD of a circle intersect externally at P. If AB=6cm,CD=3cmandPD=5cm, then the length of PB is
View Solution
