The expression √sin4(37.5)∘+4cos2(37.5)∘+√cos4(37.5)∘+4sin2(37.5)∘ simplifies to
an irrational number
a prime number
a natural number which is not composite
a real number of the form a+√b where a and b are prime
Step by step video, text & image solution for The expression sqrt(sin^(4)(37.5)^(@)+4cos^(2)(37.5)^(@)) +sqrt(cos^(4)(37.5)^(@)+4sin^(2)(37.5)^(@)) simplifies to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - RACE 1913videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Race 2110videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - RACE 1310videos
RACE
- BOOK - ALLENCHAPTER - LOGARITHMSEXERCISE - All Questions107videos
LOGARITHMS
- BOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)12videos
SEQUENCE AND PROGRESSION
Similar Questions
Knowledge Check
- Question 1 - Select One
cos51∘−sin39∘+sin37∘−cos53∘=?
A0B1Ccos104∘Dsin39∘ - Question 2 - Select One
The value of (cos53∘−sin37∘) is
A0B1C2sin37∘D2cos53∘
4 sin23∘sin37∘sin83∘=
View Solution" The value of (sin17∘)(cos13∘)+(cos17∘)(sin13∘)(cos23∘)(cos37∘)−(sin157∘)(sin37∘) is equal to
View Solution4 sin23∘sin37∘sin83∘=
View SolutionThe value of the ∣∣ ∣ ∣∣sin237∘sin253∘−tan2225∘sin253∘−tan2135∘sin237∘−tan2315∘sin237∘sin253∘∣∣ ∣ ∣∣ is
View SolutionFind the resultant of the following forces.
[sin37∘=35,cos37∘=45,sin53∘=45,cos53∘=35]
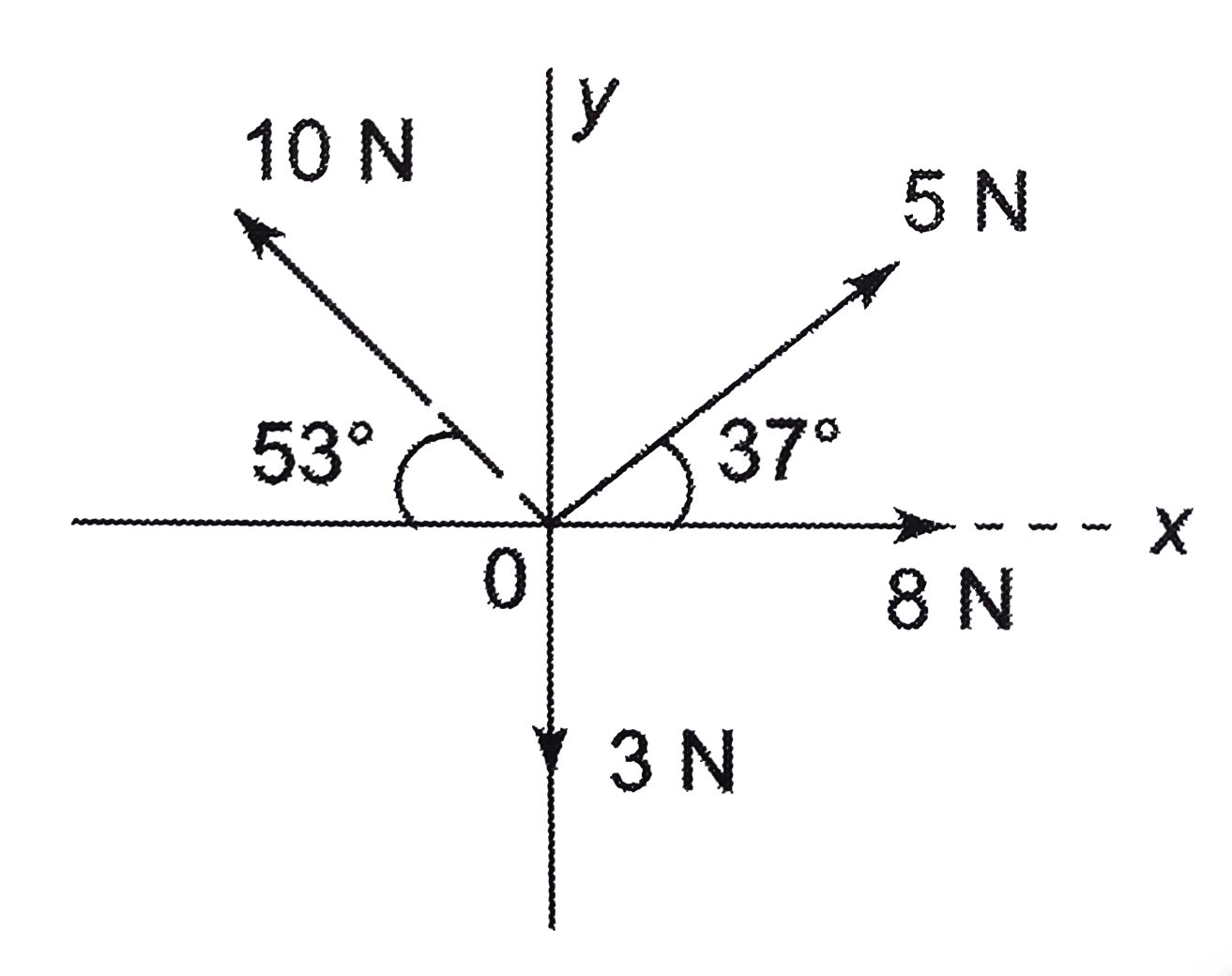 View Solution
View SolutionProve that √sin4x+4cos2x−√cos4x+4sin2x=cos2x.
View Solution

