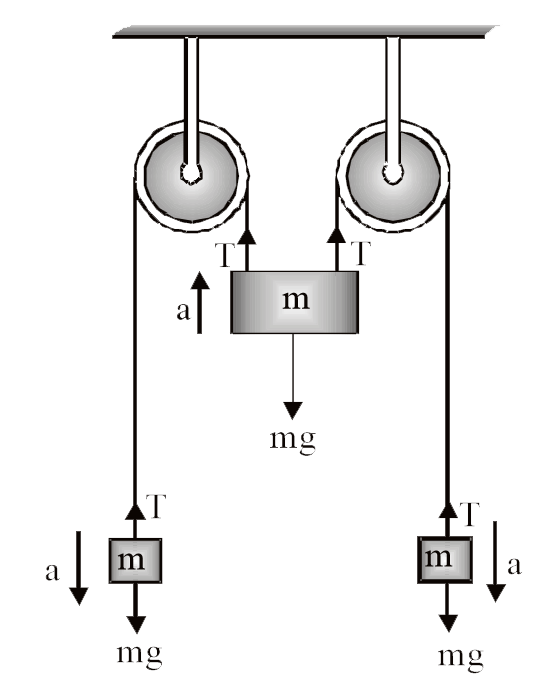
Consider the double Atwood's machine as shown in the figure
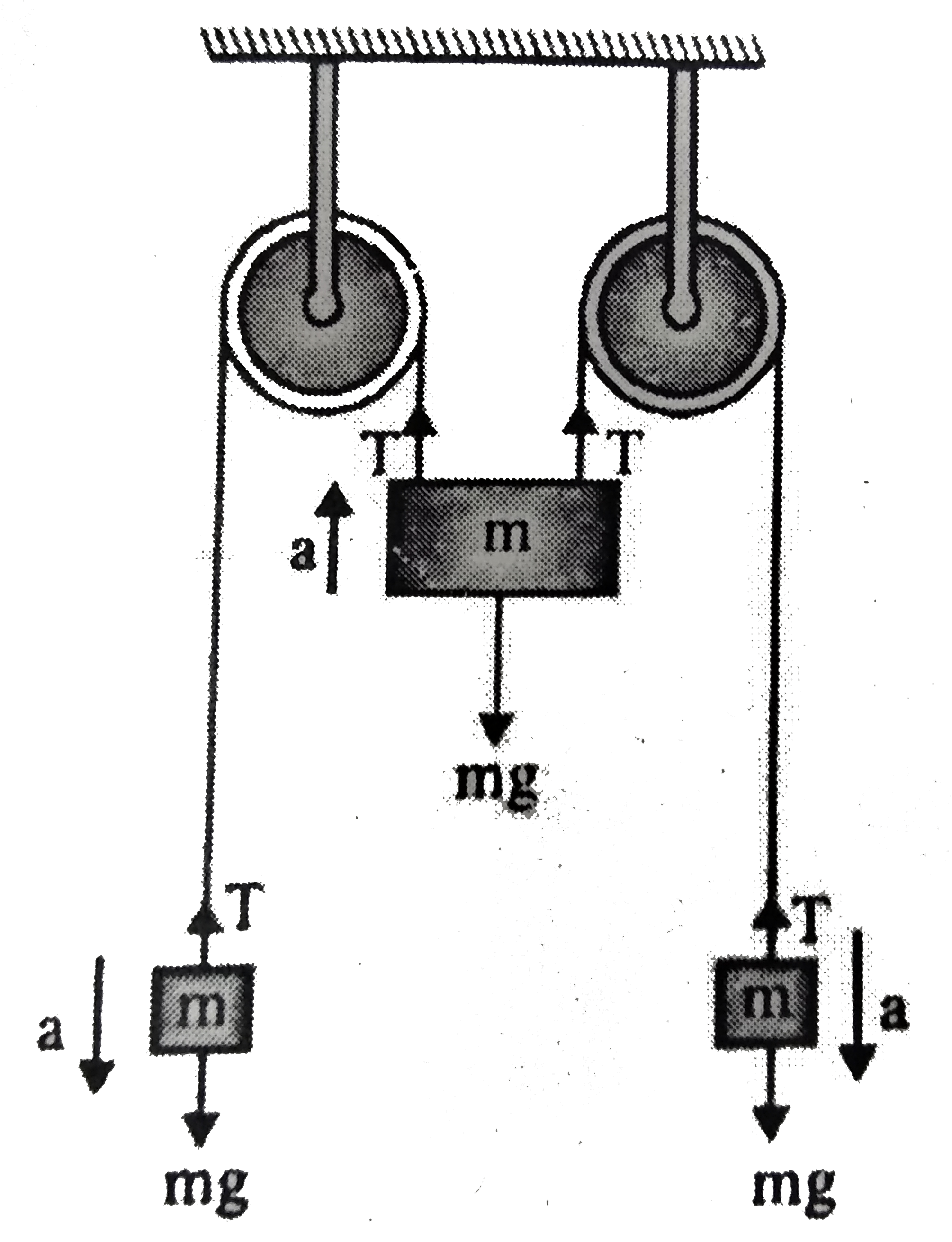
(a) What is acceleration of the masses?
(b) What is the tension in each string?
(a) Here the system behaves as a rigid system, therefore every part of the system will move with same acceleration. Thus Applying newton's law
mg−T=ma...(1)2T−mg=ma...(2)
Doubling the first equation and adding
mg=3ma⇒accelerationa=13g
(b) Tension in the string t=m(g−a)=m(g−g3)=23mg
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-1)
26 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
Knowledge Check
Consider the situation shown in the figure.
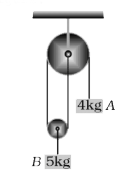
Find acceleration of B.Ag7B2g7C3g7D2g5Consider the system as shown in the figure. The pulley and the string are light and all the surfaces are frictionless. The tension in the string is (g=10m/s2) .
 A0NB1NC2ND5N
A0NB1NC2ND5N
In above question, what is the tension in each string ?
View SolutionConsider the situation shown in figure. Find the acceleration of the system and the tension in the strings.
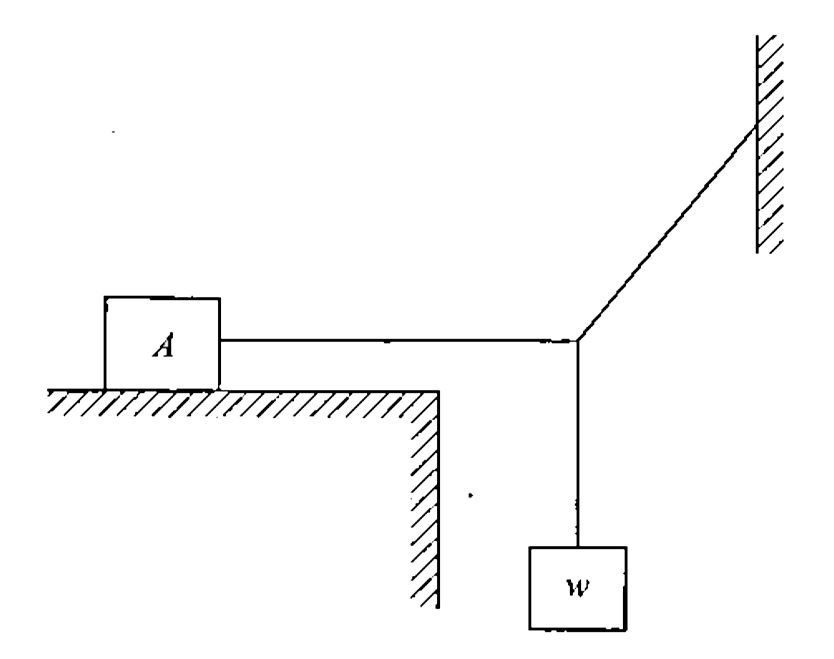
View SolutionFor the system shown in figure, the tensions in the string
View Solution
Find the common acceleration and tension in each string.
View SolutionTwo blocks shown in figure are connected by a heavy uniform rope of mass 4kg. An upward force of 200N is applied as shown
(a) What is the acceleration of the system .
(b)What is the tension at the rop of the rop ?
( c) What is the tension at the mid- point of the rop
(Takeg=9.8m/s2)

View Solution(i) Three blocks A, B and C are placed in an ideal Atwood machine as shown in the figure. When the system is allowed to move freely it was found that tension in the string connecting A to C was more than thrice the tension in the string connecting A and B. The masses of the three blocks A, B and C are m1, m2 and m3, respectively. State whether the following statements are true or false [All masses have finite non zero values and the system has a non zero acceleration].
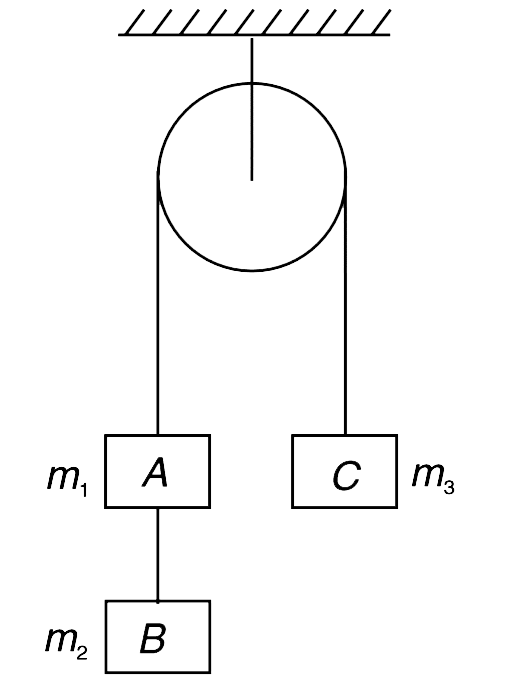
(i) m3 can have any finite value
(ii) m1>2m2
(ii) In an Atwood machine the sum of two masses is a constant. If the string can sustain a tension equal to (2430) of the weight of the sum of two masses, find the least acceleration of the masses. The string and pulley are light.
(iii) A load of w newton is to be raised vertically through a height h using a light rope. The greatest tension that the rope can bear isηw(η>1). Calculate the least time of ascent if it is required that the load starts from rest and must come to rest when it reaches a height h.
View Solution