The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

The correct Answer is:v0/cosθ
Step by step video, text & image solution for The block A is moving downward with constant velocity v_(0.) Find the velocity of the block B. When the string makes an angle theta with the horizontal by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-1)
51 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity u. As a result of this, end A starts moving down along the wall. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View Solution
Knowledge Check
If block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
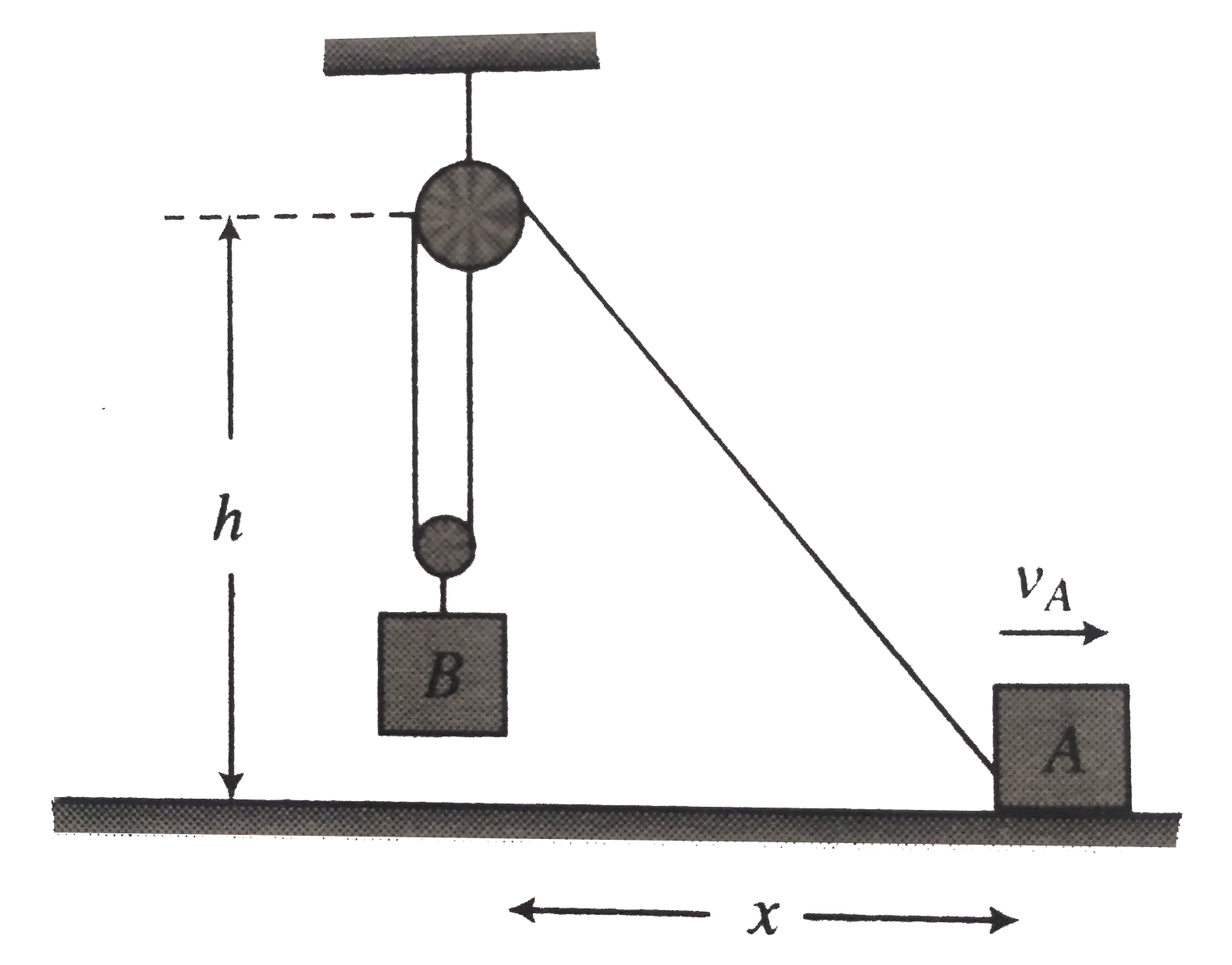 AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
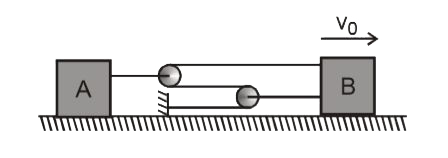
AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2Block B moves to the right with a constant velocity v0. The velocity of body A relative to B is
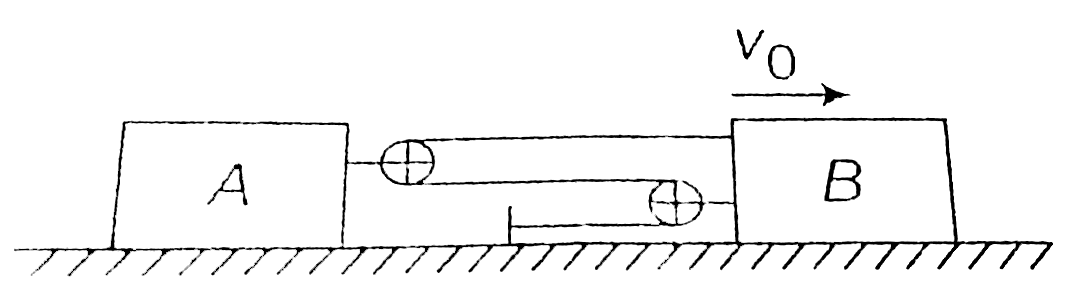 Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards right
Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards rightIn the block moves up with constant velocity v m//s. Find F
 AF=mg2BF=2mg3CF=mg3DF=m3
AF=mg2BF=2mg3CF=mg3DF=m3
The block shown is moving with constant velocity. Find μk between the block and the surface.
View Solution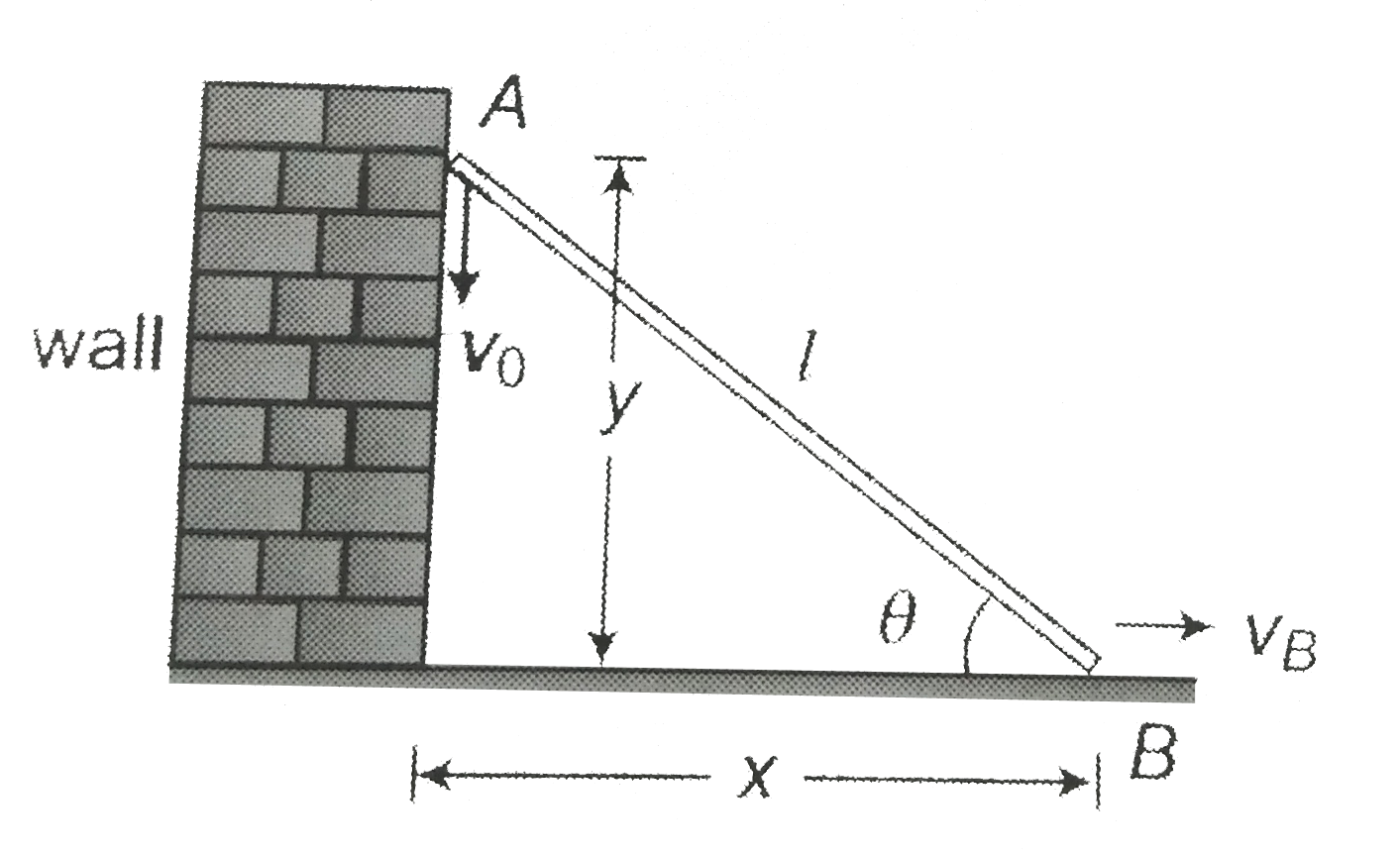
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body A relative to B is :
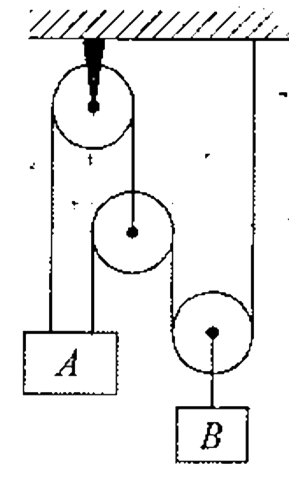
View Solution ltbgt Find the velocity of block B when ring A is moving downward with velocity v.
ltbgt Find the velocity of block B when ring A is moving downward with velocity v.
View SolutionKnowing that block B starts to move downward with a constant velocity of 18cm/sec, the velocity of block A will be:
View Solution
